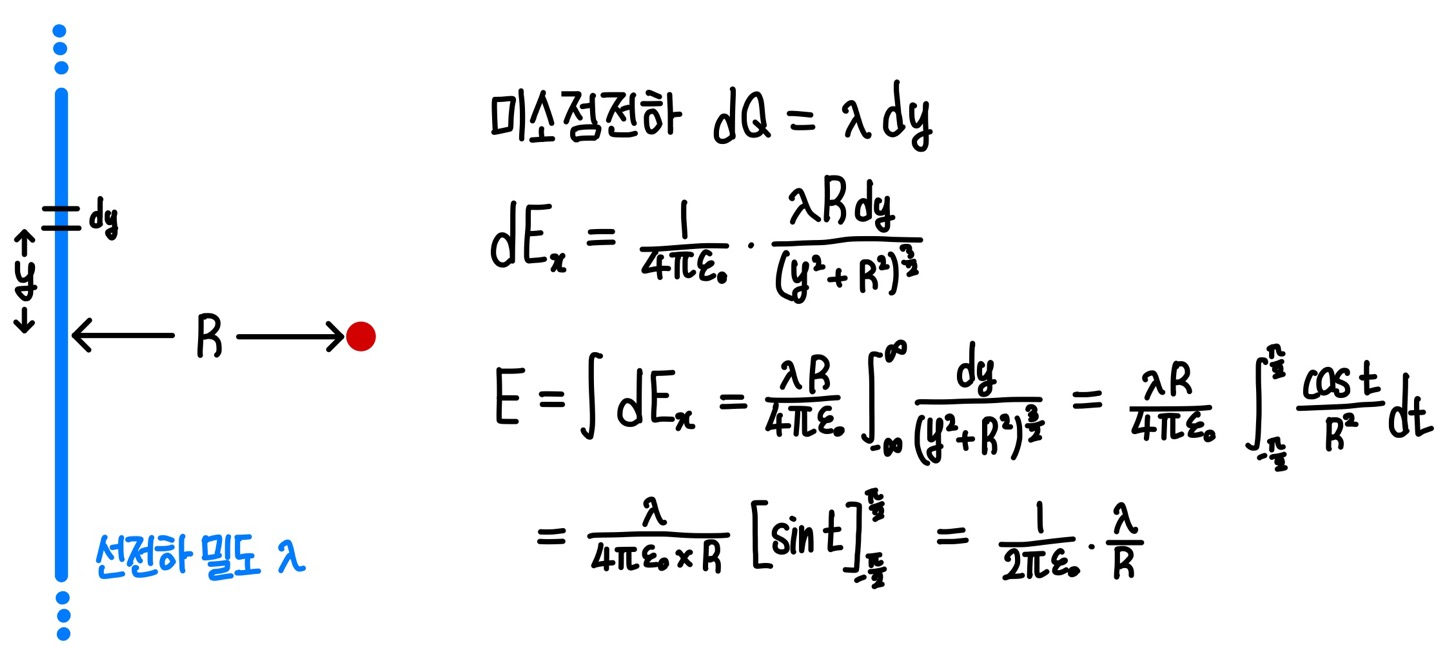점전하가 아닌 선전하나 면전하에 의한 전기장을 구할 때는, 선이나 면을 미소단위로 나누어 전기장을 미소점전하들에 의한 전기장의 합으로 생각할 수 있다.
직선 상에 있는 경우

그림과 같은 경우에서 도선의 단위길이당 전햐량, 즉 선전하밀도 $\lambda =\frac{Q}{L}$ 이다. 원점 $O$로 부터의 거리를 $x$라 하면, 미소길이 $dx$에서의 전하량 $dQ=\lambda dx$ 이다. 따라서 미소점전하 $dQ$에 의한 전기장 $dE$는 다음과 같다.
$$ dE=\frac{1}{4\pi\epsilon _0}\frac{dQ}{x^2}=\frac{1}{4\pi\epsilon _0}\frac{\lambda dx}{x^2} $$
직선 도선에 의한 전기장은 이들 미소점전하들의 합이므로 다음과 같이 구할 수 있다.
$$ \begin{align} E &= \int\, dE=\frac{\lambda}{4\pi\epsilon _0}\int_{R}^{R+L}\frac{1}{x^2}\, dx \\ &= \frac{\lambda}{4\pi\epsilon _0}\left[ -\frac{1}{x}\right] _{R}^{R+L}=\frac{1}{4\pi\epsilon _0}\frac{Q}{L}\left( \frac{1}{R}-\frac{1}{R+L}\right) \\ &= \frac{1}{4\pi\epsilon _0}\frac{Q}{R(R+L)} \end{align} $$
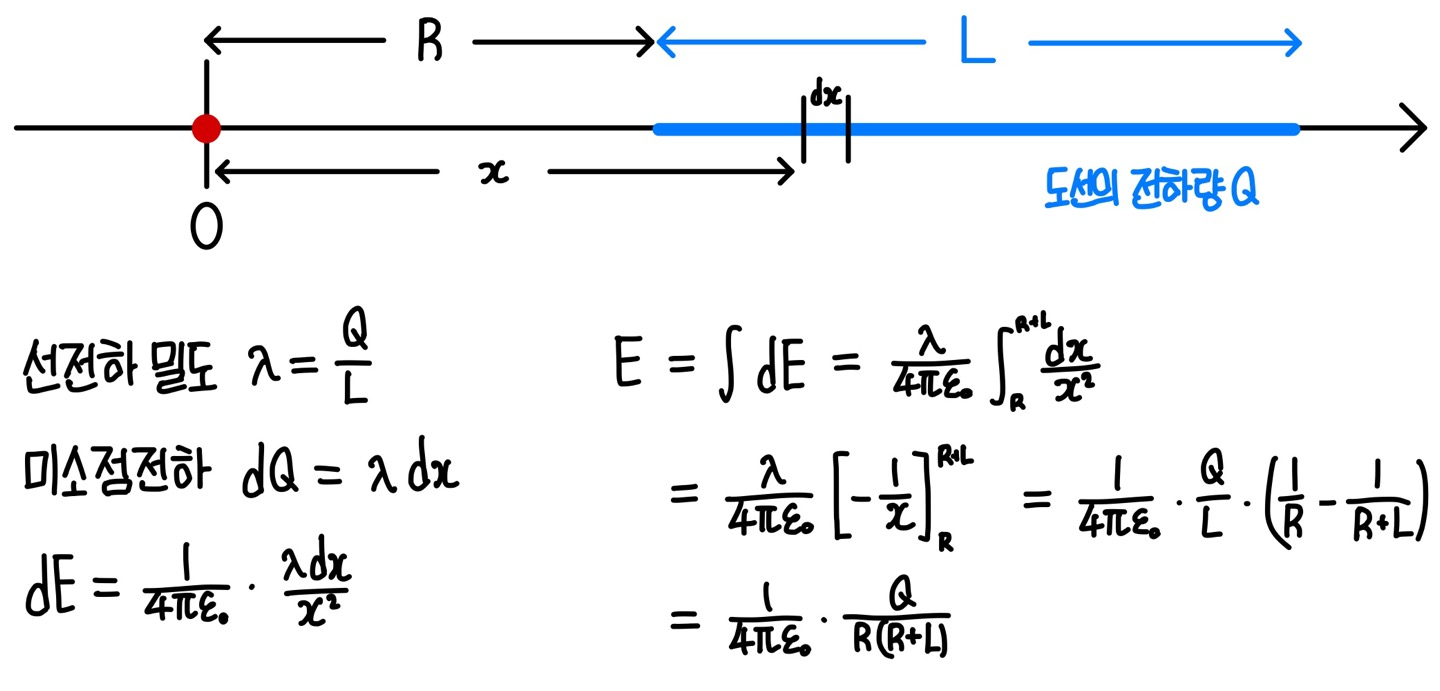
직선 상에 없는 경우
도선의 길이가 유한한 경우
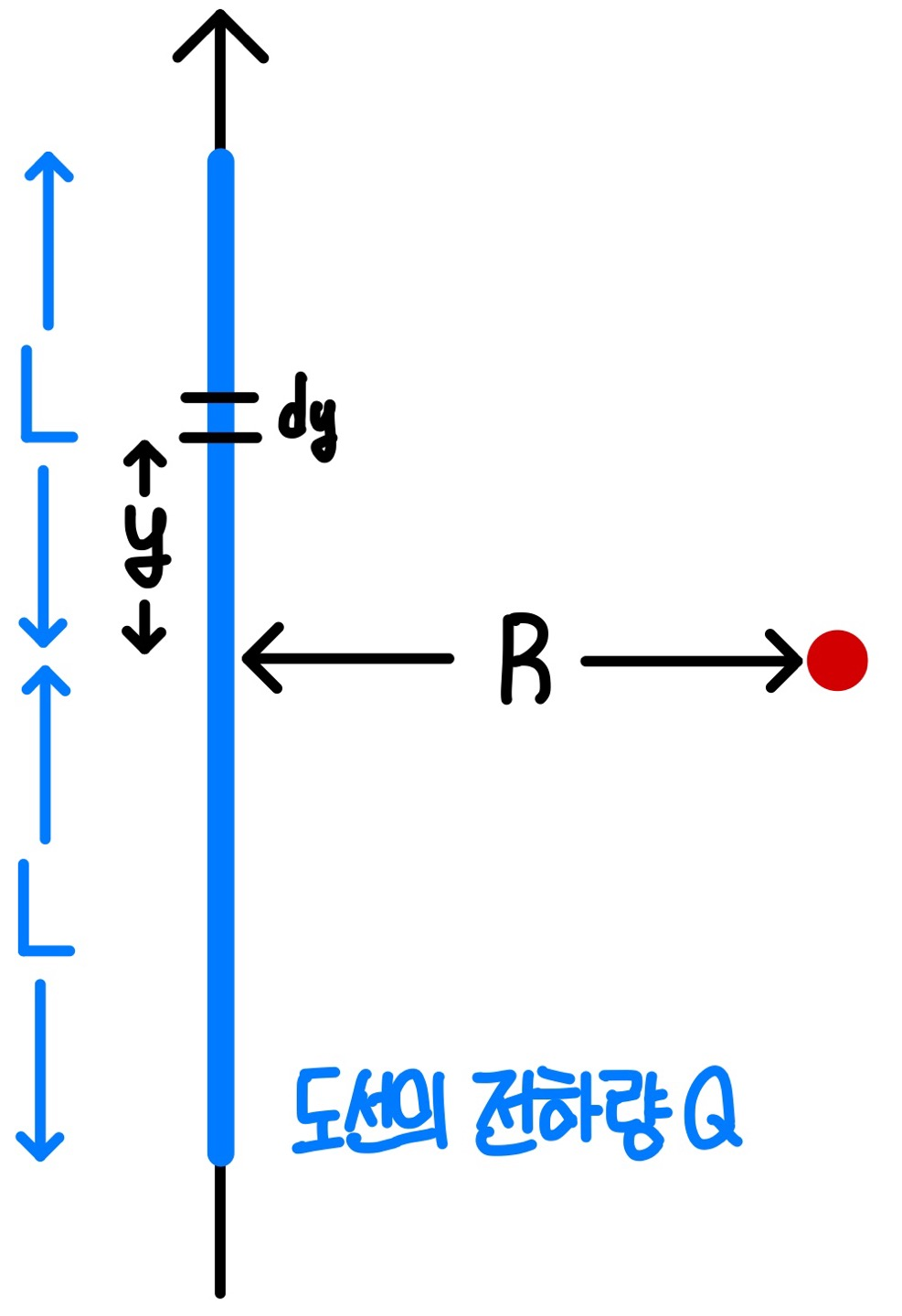
그림과 같은 경우에서 도선의 단위길이당 전햐량, 즉 선전하밀도 $\lambda =\frac{Q}{2L}$ 이다. 도선의 중심점으로 부터의 거리를 $y$이라 하면, 미소길이 $dy$에서의 전하량 $dQ=\lambda dy$ 이다. 따라서 미소점전하 $dQ$에 의한 전기장 $dE$는 다음과 같다.
$$ dE=\frac{1}{4\pi\epsilon _0}\frac{dQ}{y^2+R^2}=\frac{1}{4\pi\epsilon _0}\frac{\lambda dy}{y^2+R^2} $$
그림과 같은 경우에서 $y$축 방향 전기장 성분은 상쇄된다. 따라서 직선 도선에 의한 전기장은 이들 미소점전하들의 $x$축 성분들의 합이므로 다음과 같이 구할 수 있다.
$$ dE_x=\frac{1}{4\pi\epsilon _0}\frac{\lambda dy}{y^2+R^2}\times\frac{R}{\sqrt{y^2+R^2}}=\frac{1}{4\pi\epsilon _0}\frac{\lambda R dy}{\left( y^2+R^2\right) ^{\frac{3}{2}}} $$
$$ \begin{align} E &= \int\, dE_x=\frac{\lambda R}{4\pi\epsilon _0}\int_{-L}^{L}\frac{1}{\left( y^2+R^2\right) ^{\frac{3}{2}}}\, dy \\ &= \frac{\lambda R}{4\pi\epsilon _0}\int_{-\theta}^{\theta}\frac{\cos t}{R^2}\, dt=\frac{\lambda}{4\pi\epsilon _0\times R}\left[\sin t\right]_{-\theta}^{\theta} \\ &= \frac{1}{4\pi\epsilon _0\times R}\frac{Q}{2L}\times 2\sin\theta=\frac{1}{4\pi\epsilon _0}\frac{Q}{R\sqrt{R^2+L^2}} \end{align} $$

도선의 길이가 무한한 경우
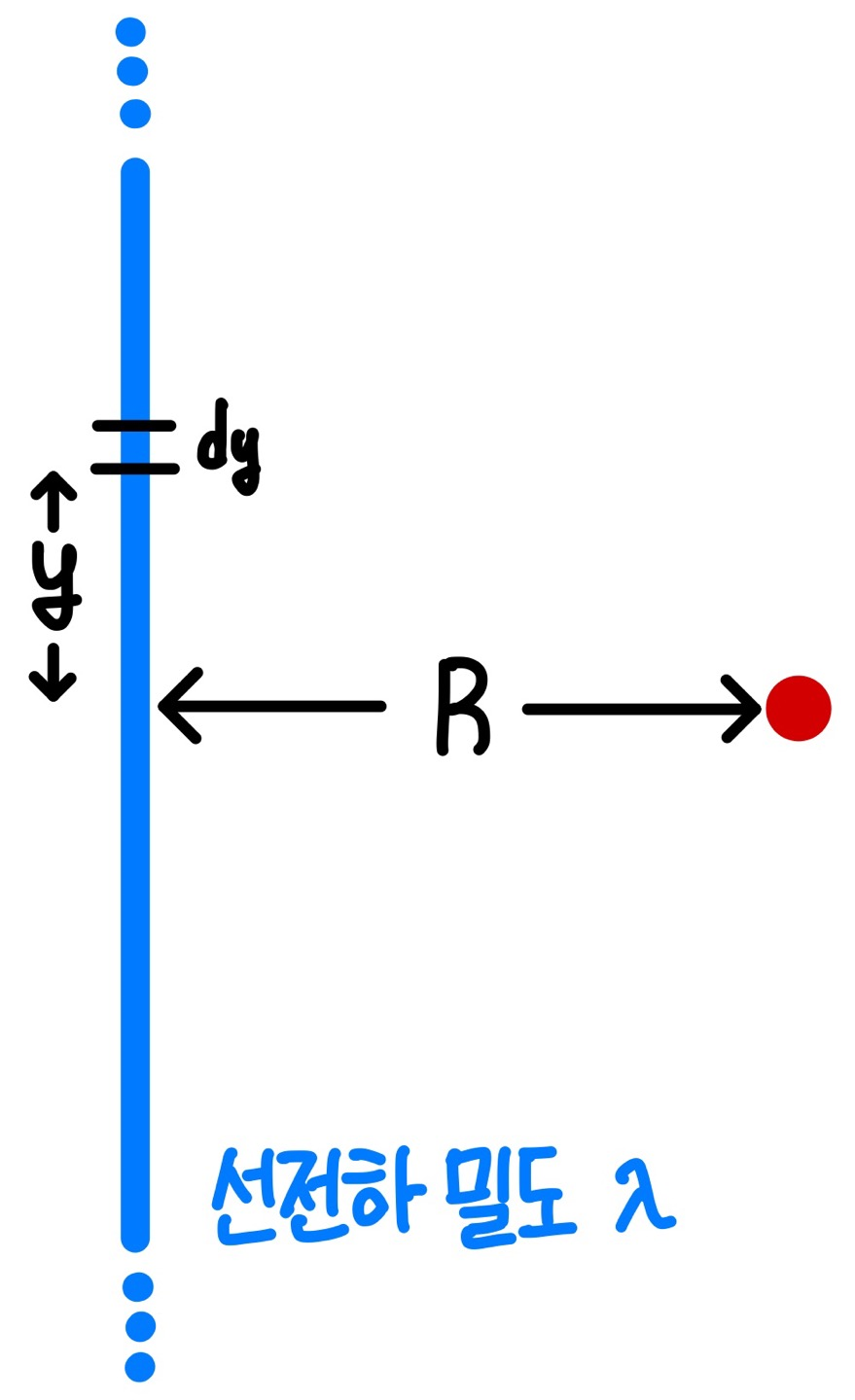
미소길이 $dy$에서의 전하량 $dQ=\lambda dy$ 이다. 따라서 미소점전하 $dQ$에 의한 전기장 $dE$는 다음과 같다.
$$ dE=\frac{1}{4\pi\epsilon _0}\frac{dQ}{y^2+R^2}=\frac{1}{4\pi\epsilon _0}\frac{\lambda dy}{y^2+R^2} $$
그림과 같은 경우에서 $y$축 방향 전기장 성분은 상쇄된다. 따라서 직선 도선에 의한 전기장은 이들 미소점전하들의 $x$축 성분들의 합이므로 다음과 같이 구할 수 있다.
$$ dE_x=\frac{1}{4\pi\epsilon _0}\frac{\lambda dy}{y^2+R^2}\times\frac{R}{\sqrt{y^2+R^2}}=\frac{1}{4\pi\epsilon _0}\frac{\lambda R dy}{\left( y^2+R^2\right) ^{\frac{3}{2}}} $$
$$ \begin{align} E &= \int\, dE_x=\frac{\lambda R}{4\pi\epsilon _0}\int_{-\infty}^{\infty}\frac{1}{\left( y^2+R^2\right) ^{\frac{3}{2}}}\, dy \\ &= \frac{\lambda R}{4\pi\epsilon _0}\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\frac{\cos t}{R^2}\, dt=\frac{\lambda}{4\pi\epsilon _0\times R}\left[\sin t\right]_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \\ &= \frac{1}{2\pi\epsilon _0}\frac{\lambda}{R} \end{align} $$