벡터 장에서의 선적분
벡터 함수의 선적분은 스칼라 장에서의 선적분과 다르게 적분식에 Dot Product가 포함된다.
$$ \int_{C}F\, dr\quad\longleftrightarrow\quad\int_{C}\vec{F}\cdot\, d\vec{r} $$
$ \vec{F} =F_x\hat{x} +F_y\hat{y} $ ($F_x$, $F_y$는 $x$, $y$에 대한 함수) 와 같이 주어졌을 때,
$$ d\vec{r} =dx\hat{x} +dy\hat{y} $$
$$ \vec{F}\cdot d\vec{r} =\left( F_{x}, F_{y} \right)\cdot\left( dx, dy \right) =F_{x}dx+F_{y}dy $$
$$ \int_{C}\vec{F}\cdot\, d\vec{r} =\int_{C}\left( F_{x}dx+F_{y}dy\right) $$
이렇게 얻은 식을 곡선 $C$의 결정 조건을 이용해 하나의 변수로 정리하여(또는 매개변수화하여) 풀면 된다.
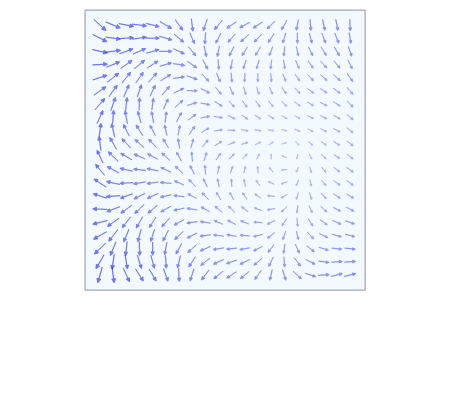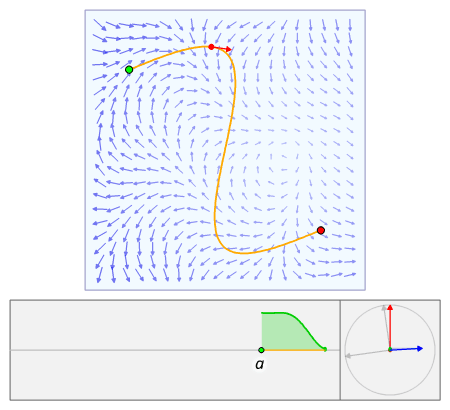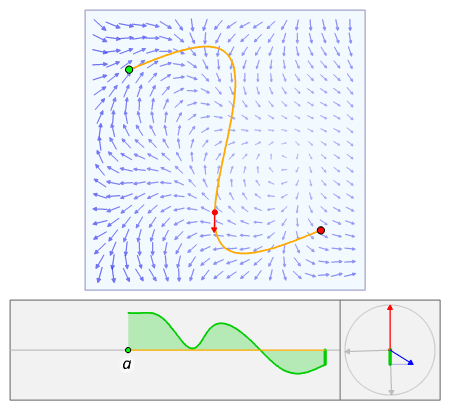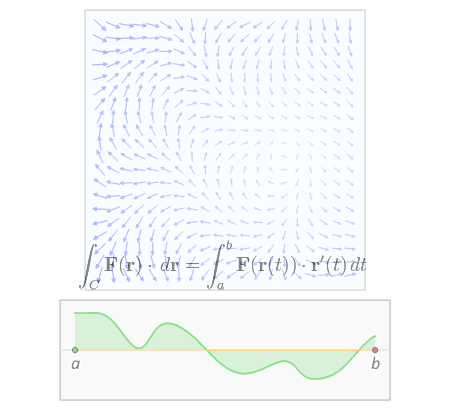
위와 같은 선적분의 정성적인 의미를 생각해보면, 아래의 애니메이션과 같이 곡선 위의 모든 점들에 대해 그 점에서 곡선의 접선 방향의 성분을 적분한 것과 같음을 알 수 있다.
예제
$ \vec{F} =xy\hat{x} -y^2\hat{y} $와 같이 주어지고 곡선 $ C : y=\frac{1}{4}x^2 \ (0\le x\le 2) $ 일 때, $ \int_{C}\vec{F}\cdot\, d\vec{r} $를 구하여라.
step1. 선적분 식 세우기
$$ d\vec{r} =dx\hat{x} +dy\hat{y} $$
$$ \vec{F}\cdot d\vec{r} =\left( xy, -y^2 \right)\cdot\left( dx, dy \right) =xydx-y^2dy $$
$$ \int_{C}\vec{F}\cdot\, d\vec{r} =\int_{C}\left( xydx-y^2dy\right) $$
step2. 하나의 변수로 정리
$ y=\frac{1}{4}x^2 $로부터 주어진 적분식을 x에 대한 식으로 나타내면
$$ dy=\frac{1}{2}xdx $$
$$ \int_{C}\vec{F}\cdot\, d\vec{r} =\int_{C}\left( xydx-y^2dy\right)=\int_{0}^{2}\left\{ x\left(\frac{1}{4}x^2\right) dx-\left(\frac{1}{4}x^2\right) ^2\left(\frac{1}{2}xdx\right)\right\}=\int_{0}^{2}\left(\frac{1}{4}x^3-\frac{1}{32}x^5\right)\, dx $$
step3. 정적분 계산
$$ \int_{0}^{2}\left(\frac{1}{4}x^3-\frac{1}{32}x^5\right)\, dx=\left[\frac{1}{16}x^4-\frac{1}{192}x^6\right]_{0}^{2}=\frac{2}{3} $$
