정의
델 연산자는 $\nabla$와 같이 나타내며 아래와 같이 정의된다.
$$ \nabla =\sum_{i=1}^n \frac{1}{h_{i}}\frac{\partial}{\partial x_{i}}\hat{x_{i}} $$
이처럼 델 연산자는 벡터로 취급하여도 무방하다.
$h_{i}$는 Scaling Factor이며 극좌표계, 원통좌표계, 구면좌표계와 같이 서로 직교하는 좌표계에서는 $h_{i}$만큼 보정하여 계산한다.
직교좌표계 : $h_{x}=1$, $h_{y}=1$, $h_{z}=1$
구면좌표계 : $h_{r}=1$, $h_{\theta}=r$, $h_{\rho}=r\sin\theta$
원통좌표계 : $h_{\rho}=1$, $h_{\theta}=r$, $h_{z}=1$
따라서 직교좌표계에서는 다음과 같다. 이 글에서는 직교좌표계의 상황만을 다룬다.
$$ \nabla =\sum_{i=1}^n \frac{1}{h_{i}}\frac{\partial}{\partial x_{i}}\hat{x_{i}} =\frac{\partial}{\partial x}\hat{x} +\frac{\partial}{\partial y}\hat{y} +\frac{\partial}{\partial z}\hat{z} $$
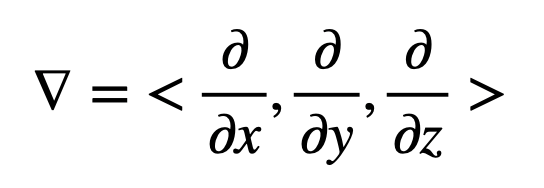
Gradient (그래디언트, 기울기벡터)
$$ \nabla f=\left(\frac{\partial}{\partial x}\hat{x} +\frac{\partial}{\partial y}\hat{y} +\frac{\partial}{\partial z}\hat{z}\right)f=\frac{\partial f}{\partial x}\hat{x} +\frac{\partial f}{\partial y}\hat{y} +\frac{\partial f}{\partial z}\hat{z} $$
기울기벡터라고도 하며, 스칼라 함수의 변화량을 알기 위해 사용된다. $\nabla$를 벡터로 취급하면 이는 벡터의 Multiplication 연산과 같다.
Divergence (다이버전스, 발산)
$$ \nabla\cdot\vec{u} =\left(\frac{\partial}{\partial x}\hat{x} +\frac{\partial}{\partial y}\hat{y} +\frac{\partial}{\partial z}\hat{z}\right)\cdot\left(u_{x}\hat{x} +u_{y}\hat{y} +u_{z}\hat{z}\right) =\frac{\partial u_{x}}{\partial x} +\frac{\partial u_{y}}{\partial y} +\frac{\partial u_{z}}{\partial z} $$
발산이라고도 하며, 어떤 국소적인 지점에서 유입되거나 유출되는 벡터장의 선속을 나타낸다. $\nabla$를 벡터로 취급하면 이는 벡터의 Dot Product와 같다.
Curl (컬, 회전)
$$ \begin{align} \nabla\times\vec{u} &=\left(\frac{\partial}{\partial x}\hat{x} +\frac{\partial}{\partial y}\hat{y} +\frac{\partial}{\partial z}\hat{z}\right)\times\left(v_{x}\hat{x} +v_{y}\hat{y} +v_{z}\hat{z}\right) =\begin{vmatrix} \hat{x} & \hat{y} & \hat{z} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ v_{x} & v_{y} & v_{z} \end{vmatrix} \\ &=\left(\frac{\partial v_{z}}{\partial y} -\frac{\partial v_{y}}{\partial z}\right)\hat{x} +\left(\frac{\partial v_{x}}{\partial z} -\frac{\partial v_{z}}{\partial x}\right)\hat{x} +\left(\frac{\partial v_{y}}{\partial x} -\frac{\partial v_{x}}{\partial y}\right)\hat{x} \end{align} $$
회전이라고도 하며, 어떤 국소적인 영역의 단위면적 당 벡터장의 선속이 회전하는 양을 나타낸다. $\nabla$를 벡터로 취급하면 이는 벡터의 Cross Product와 같다.
Laplace Operator
라플라스 연산자(라플라시안)는 2차 미분연산자의 일종으로, 스칼라 함수의 경우 기울기벡터의 발산으로 정의된다. 기호 $\vartriangle$ 또는 $\nabla^{2}$ 를 사용하여 나타낸다.
$$ \nabla^{2} f=\nabla\cdot\left(\nabla f\right) $$
직교좌표계에서 라플라시안은 다음과 같다.
$$ \nabla^{2} f=\nabla\cdot\left(\nabla f\right) =\left(\frac{\partial}{\partial x}\hat{x} +\frac{\partial}{\partial y}\hat{y} +\frac{\partial}{\partial z}\hat{z}\right)\cdot\left(\frac{\partial f}{\partial x}\hat{x} +\frac{\partial f}{\partial y}\hat{y} +\frac{\partial f}{\partial z}\hat{z}\right) =\frac{\partial^{2}f}{\partial x^{2}} +\frac{\partial^{2}f}{\partial y^{2}} +\frac{\partial^{2}f}{\partial z^{2}} $$
Vector Laplacian
$\nabla$를 벡터로 취급하면 Vector Triple Product로부터 $ \nabla\times\left(\nabla\times\vec{A}\right) =\nabla\left(\nabla\cdot\vec{A}\right) -\nabla\cdot\left(\nabla\vec{A}\right) $ 가 성립한다.
이로부터 벡터의 라플라시안은 다음과 같이 정의된다.
$$ \nabla^{2}\vec{A} =\nabla\cdot\left(\nabla\vec{A}\right) =\nabla\left(\nabla\cdot\vec{A}\right) -\nabla\times\left(\nabla\times\vec{A}\right) $$
