선적분의 개념과 정의

 

선적분 Line Integral

 

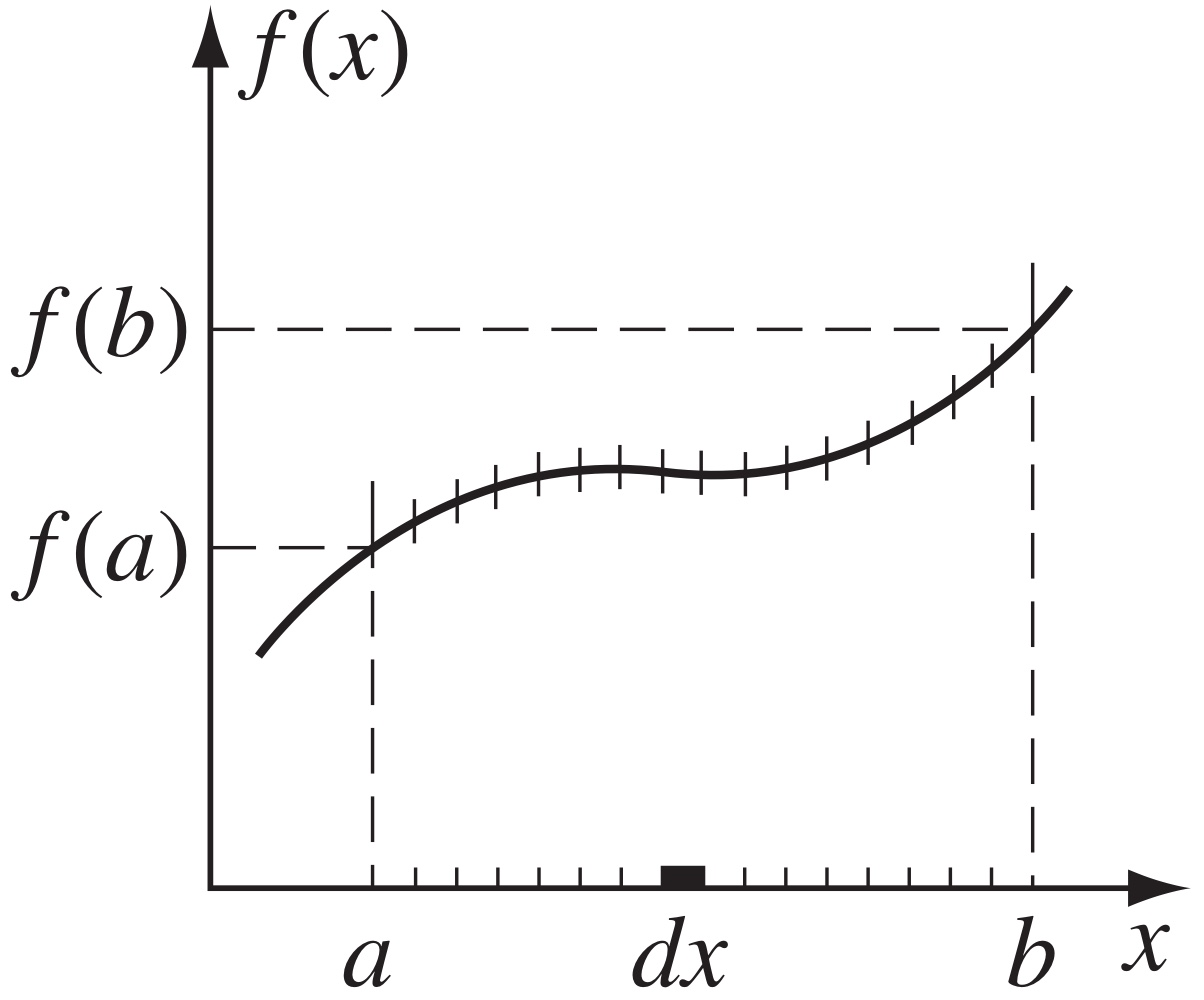
일반적인 정적분의 경우, 한 직선 위에 존재하는 모든 점들에 대한 적분으로 생각할 수 있다. 예를 들자면

$$\int_{a}^{b} f(x)\, dx$$

와 같이 주어진 정적분의 경우 적분 구간에 속하는 x축 상의 모든 점들에 대한 함수 $f(x)$의 적분을 구하는 것이 된다.

 

이와 다르게 선적분은, 임의의 곡선 위에 존재하는 모든 점들에 대한 적분을 구하는 것이다.

임의의 곡선 $C$가 다음과 같이 주어졌다고 하면,

 

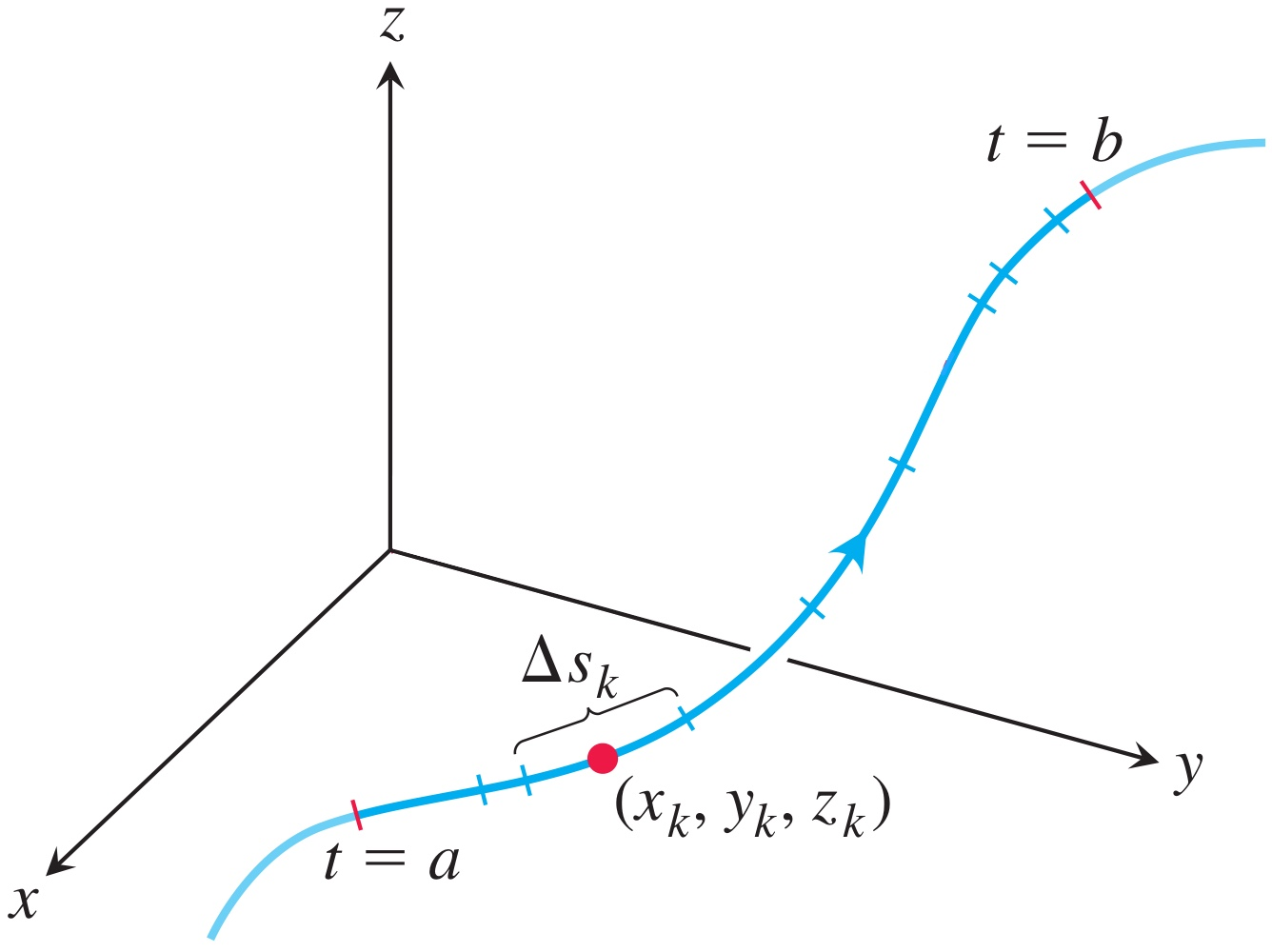
닫힌 구간 $\left[ a, b\right]$에서 함수 $f\left( x_{t}, y_{t}, z_{t}\right)$에 대해 구간 $\left[ a, b\right]$를 $n$분할하여 $a$부터 $b$까지의 각 분할점을 $a=t_{0}<t_{1}<t_{2}<\cdots <t_{n}=b$ 라 하자.

이때 각 소구간 $\left[ t_{k-1}, t_{k}\right]$에서 해당 구간의 오른쪽 끝점 $t_{k}$와 구간의 길이 $\Delta s_{k}=t_{k}-t_{k-1}$에 대하여 다음의 합을 정의한다.

$$R_{}n=\sum_{k=1}^{n} f\left( x_{k}, y_{k}, z_{k}\right)\Delta s_{k}$$

마찬가지로 각 소구간에서 해당 구간의 왼쪽 끝점 $t_{k-1}$에 대하여 다음의 합을 정의한다.

$$R_{}n=\sum_{k=1}^{n} f\left( x_{k-1}, y_{k-1}, z_{k-1}\right)\Delta s_{k}$$

 

$lim_{\parallel p\parallel\to 0} R_n=lim_{\parallel p\parallel\to 0} L_n=S\quad (\parallel p\parallel =Max(\Delta x_k);\;norm)$ 에서 $S=\lim_{n\to\infty}\sum_{k=1}^{n} f\left( x_{k}, y_{k}, z_{k}\right)\Delta s_{k}$가 성립한다.

 

 

 

 

따라서 곡선 $C$에 대한 함수 $f$의 선적분은 다음과 같이 정의된다.

| DEFINITION |
$$\int_{C}f\left( x, y, z\right)\, ds=\lim_{n\to\infty}\sum_{k=1}^{n} f\left( x_{k}, y_{k}, z_{k}\right)\Delta s_{k}$$

 

 

$ds$는 곡선 $C$의 미소길이로서 $ds=\sqrt{\left( dx\right)^{2}+\left( dy\right)^{2}+\left( dz\right)^{2}}=\sqrt{\left(\frac{dx}{dt}\right)^{2}+\left(\frac{dy}{dt}\right)^{2}+\left(\frac{dz}{dt}\right)^{2}}dt$ 이므로 선적분은 다음과 같이 계산할 수 있다.

 

$$\int_{C}f\left( x, y, z\right)\, ds=\int_{a}^{b}f\left( x(t), y(t), z(t)\right)\sqrt{\left(\frac{dx}{dt}\right)^{2}+\left(\frac{dy}{dt}\right)^{2}+\left(\frac{dz}{dt}\right)^{2}}\, dt$$