복소수 Complex Number
실수 : 유리수와 무리수를 통튼 것
허수 : $x$에 대한 이차방정식 $x^2=-1$의 해 $i$와 실수의 곱으로서 표현되는 수
복소수란 실수와 허수의 합의 꼴로서 표현되는 수이다. 즉 모든 복소수는 두 실수 $a$, $b$에 대하여 아래와 같이 표현된다.
$$ a+bi\quad \left( a, b\in\mathbb{R} \right) $$
- 복소수 $z=a+bi$에 대해 $a$를 실수부, $b$를 허수부라고 한다.
- 실수는 $b=0$ 인 복소수이고, 허수는 $b\ne 0$ 인 복소수이다. 이때 $a=0$ 이고 $b\ne 0$ 인 복소수를 순허수라고 한다.
- 복소수 $z=a+bi$ 에 대하여 $a-bi$ 를 $z$의 켤레복소수 $\bar{z}$라고 한다.
- 복소수 전체의 집합은 주로 $ \mathbb{C} $ 로 나타낸다.
복소수의 덧셈
두 복소수 $z=a+bi$, $w=c+di$ 에 대하여 $z$와 $w$의 덧셈은 아래와 같이 정의 된다.
$$ z+w=\left( a+bi\right)+\left( c+di\right) =\left( a+c\right)+\left( b+d\right) i $$
식을 보면 실수 성분과 허수 성분끼리의 합과 같다. 이는 벡터의 덧셈 연산 방법과 동일하다. 이를 통해 가로축을 실수부, 세로축을 허수부로 둔 좌표계에서 복소수는 직교좌표계에서의 위치벡터와 같이 해석할 수 있음을 알 수 있다.

복소평면 Complex Plane
복소평면이란 복소수를 대응시킨 평면을 말하며 가우스 평면, 복소수 평면이라고도 한다.
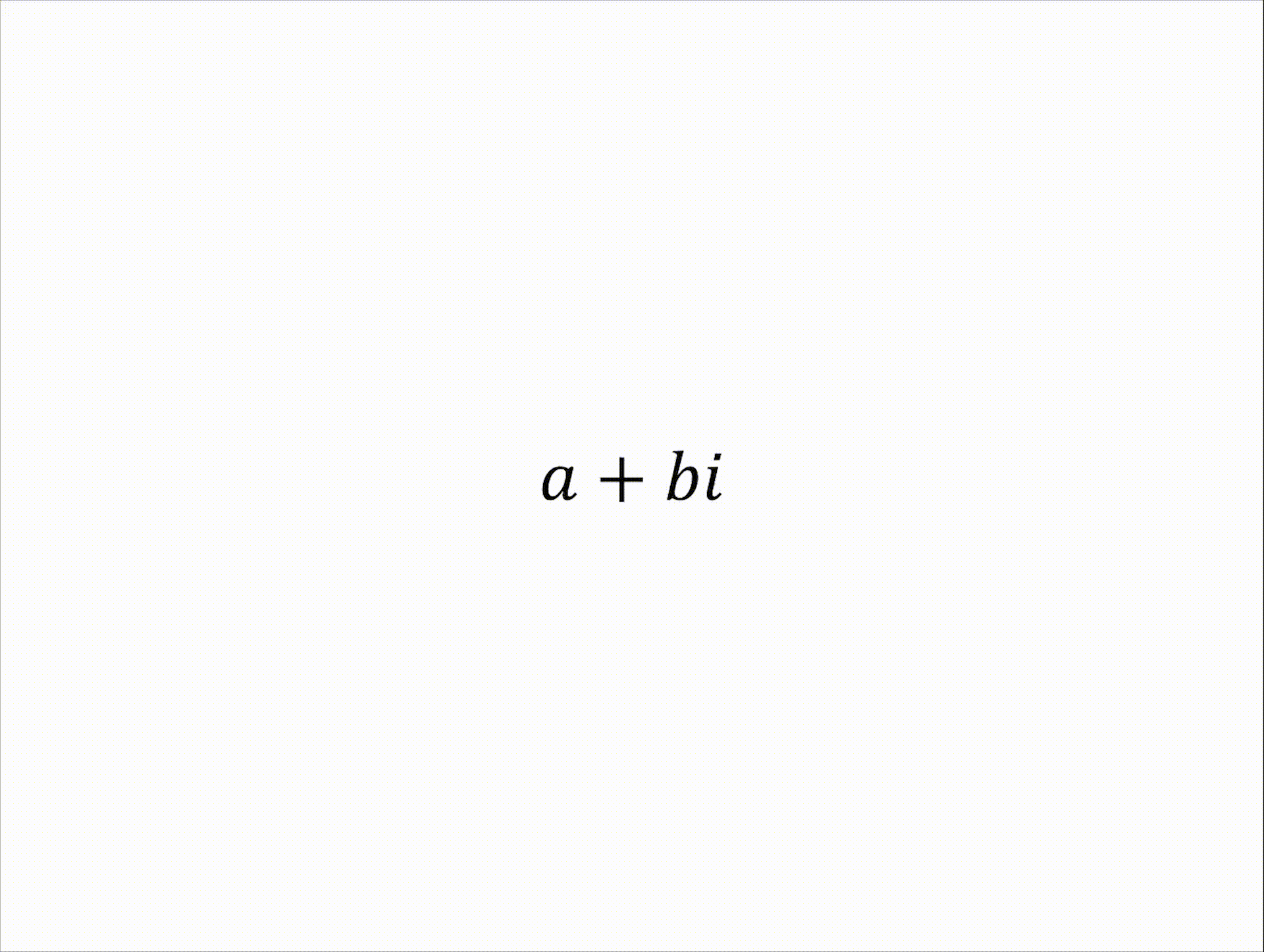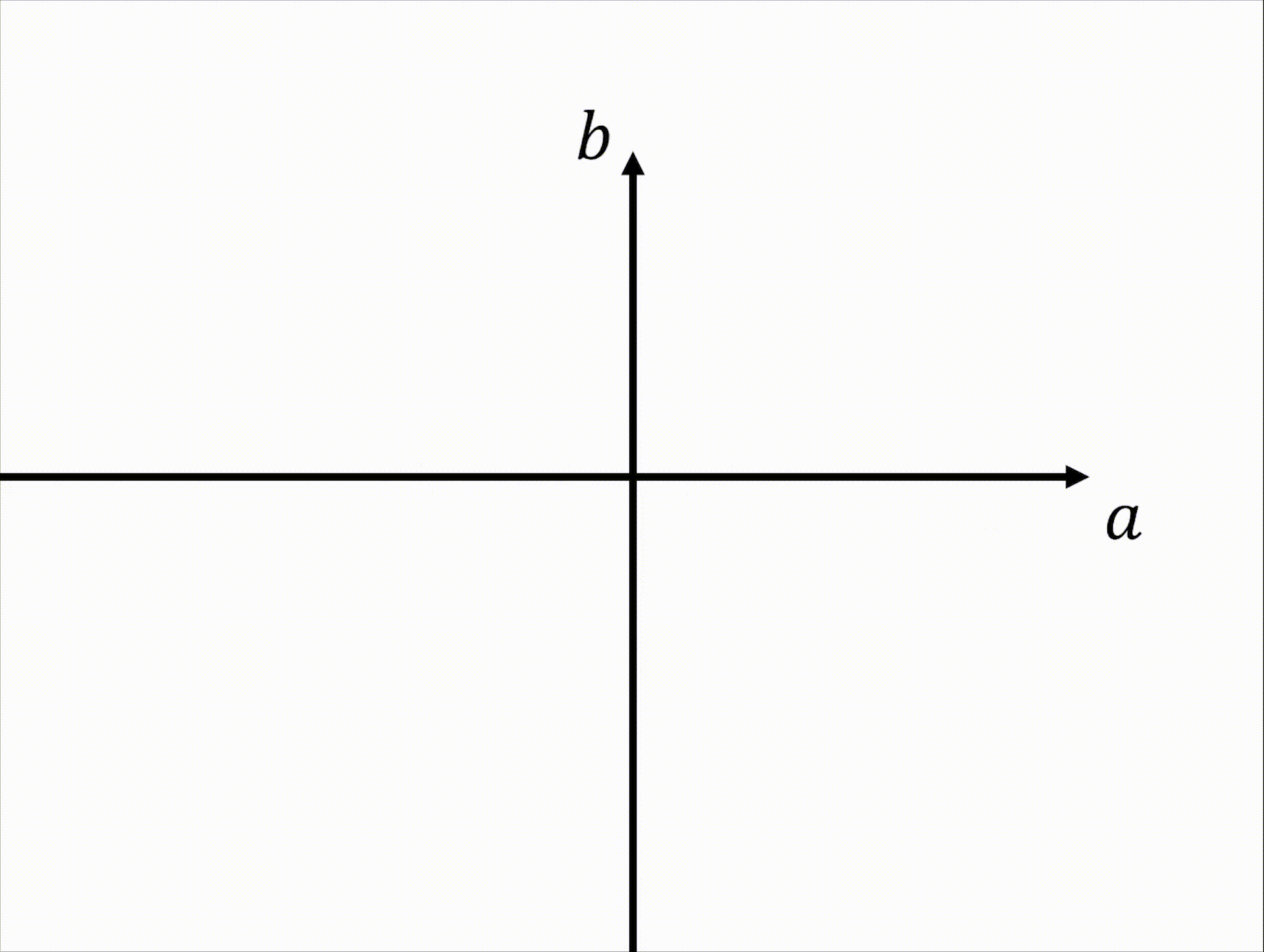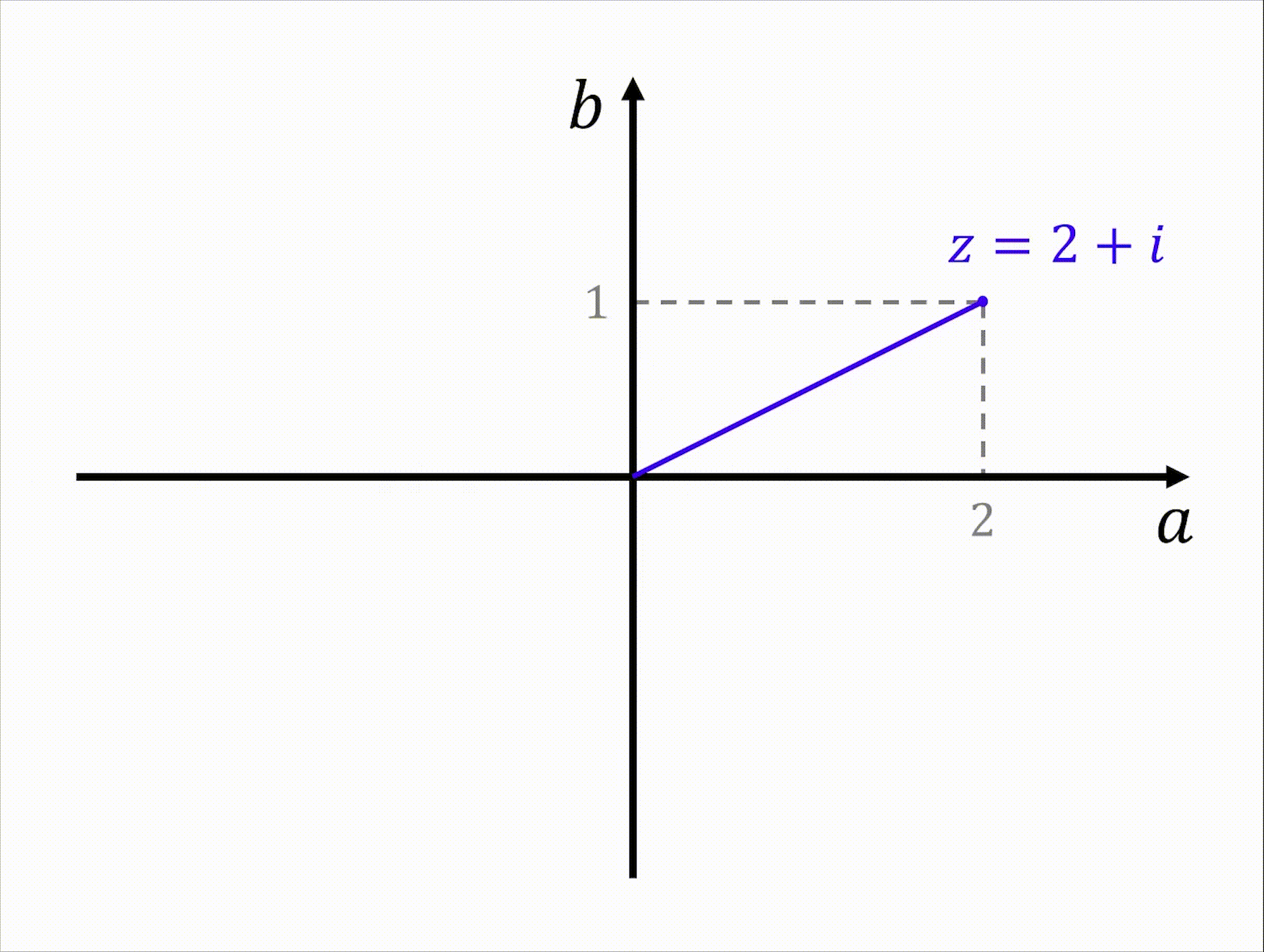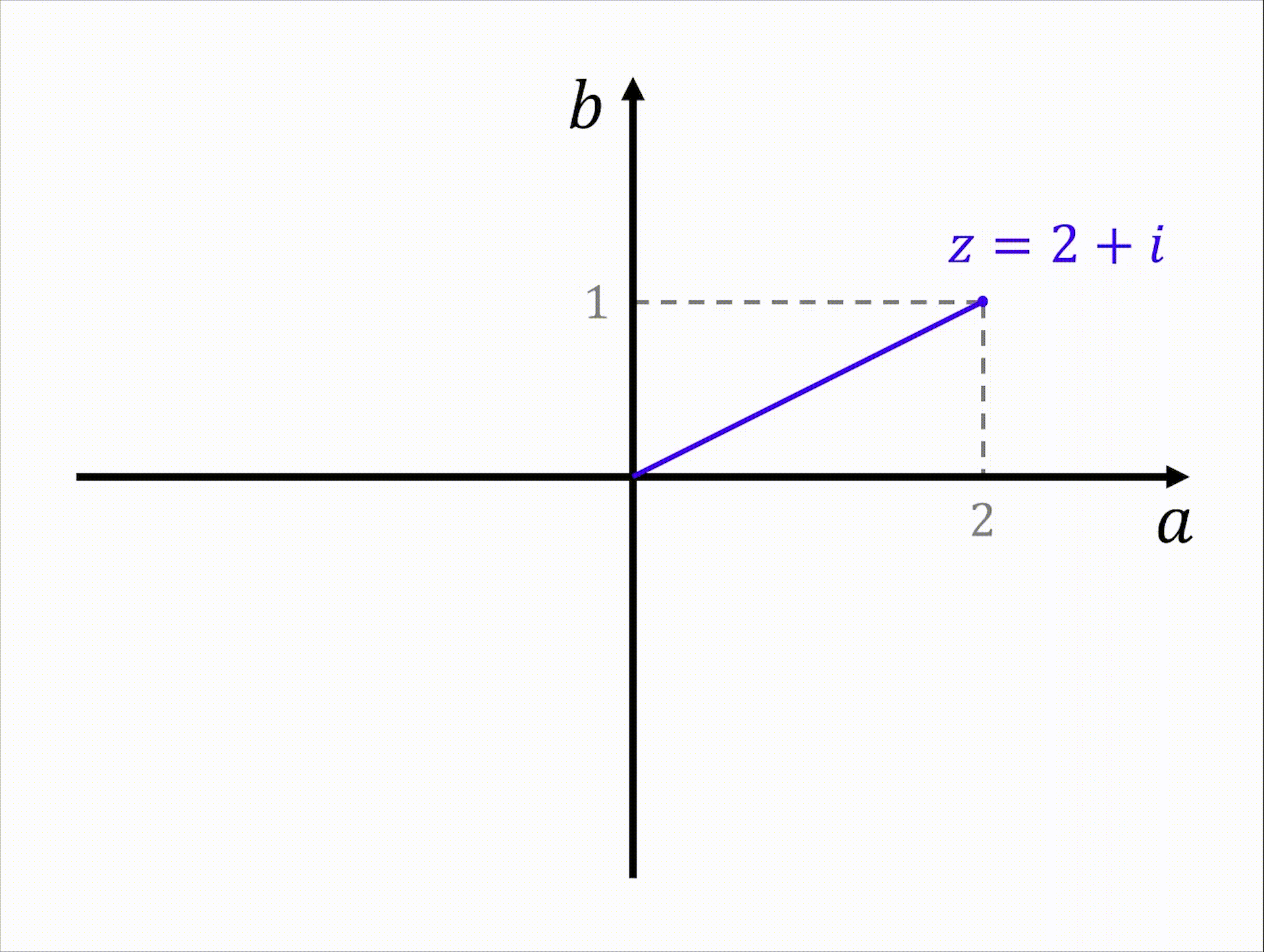
복소수의 실수부를 좌표평면의 가로축, 허수부를 세로축에 대응시킨다고 생각해보자. 복소수 $z=a+bi$ 의 실수부 $a$와 허수부 $b$는 실수이므로 복소수 전체의 집합과 좌표평면 위의 점 전체의 집합은 서로 일대일 대응 관계가 될 것이다.
$$ z=a+bi\ \leftrightarrow\ P\left( a, b\right)\qquad\cdots\left( a, b\in\mathbb{R}\right) $$
이러한 대응관계에 의하여 복소수 집합 $\mathbb{C}$를 좌표평면 ${\mathbb{R}}^{2}$에 나타낼 수 있는 것이다.
복소평면에서 복소수 $z=a+bi$를 나타내는 점을 기호로 $P\left( a, b\right)$ 나 $P\left( z\right)$ 와 같이 나타낸다.
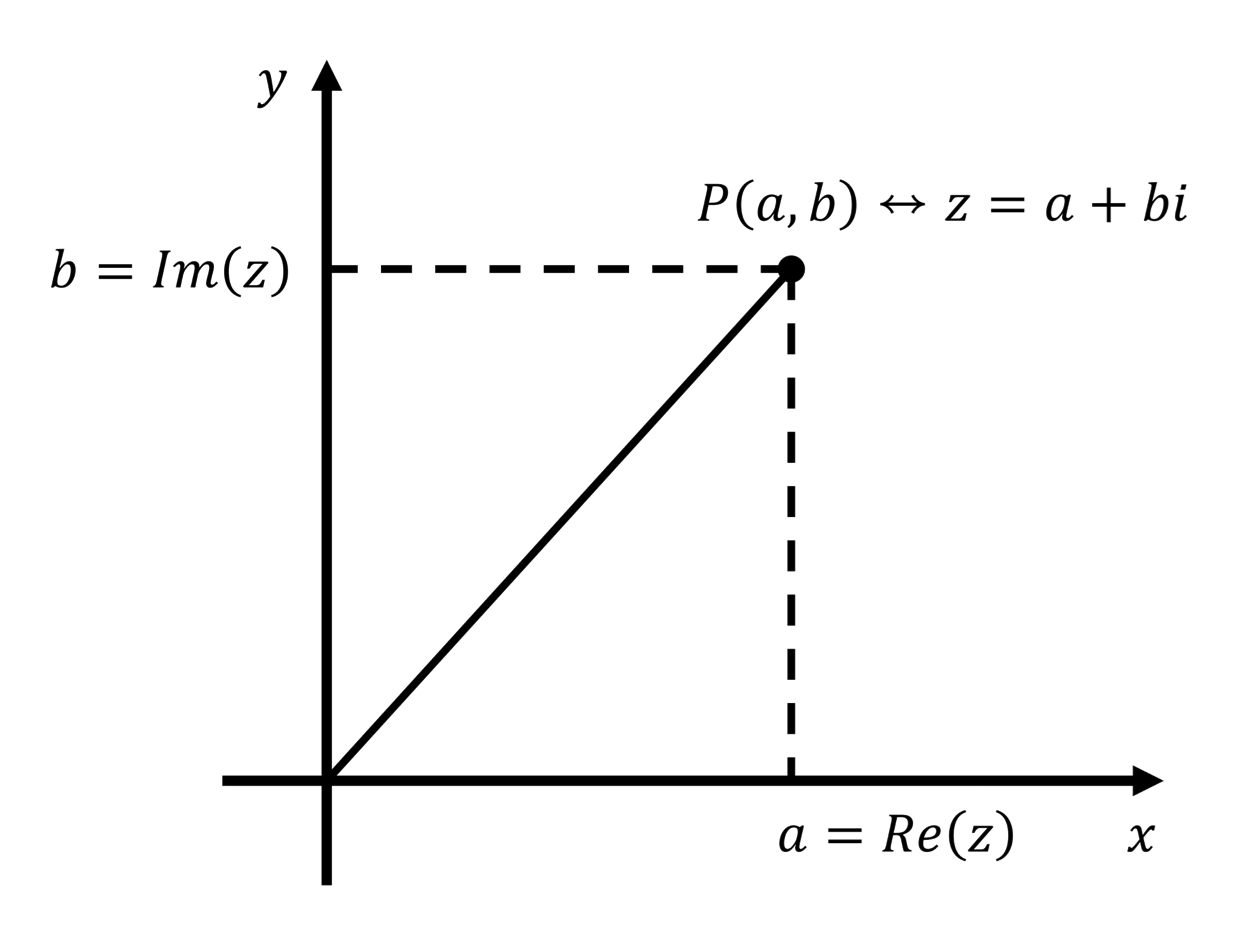
실수부와 허수부
복소수 $z=a+bi$ 의 실수부는 $z$에 대응하는 복소평면 위의 점 $P\left( a, b\right)$ 의 $x$좌표와 같다. 이를 아래와 같이 표현한다.
$$ Re\left( z\right) =a $$
복소수 $z=a+bi$ 의 실수부는 $z$에 대응하는 복소평면 위의 점 $P\left( a, b\right)$ 의 $x$좌표와 같다. 이를 아래와 같이 표현한다.
$$ Im\left( z\right) =b $$
여기서 Re, Im은 각각 Real과 Imaginary의 약어이다.
실수는 $Im\left( z\right) =0$ 인 복소수로, 복소수 $z$가 실수이기 위한 필요충분조건은 $z=\bar{z}$ 이다.
순허수는 $Re\left( z\right) =0$ 이고 $Im\left( z\right)\ne 0$ 인 복소수로, 복소수 $z$가 순허수이기 위한 필요충분조건은 $z=-\bar{z}$ 이다.
실수축과 허수축
복소평면 위에서 실수 $a=a+0i$는 $x$축 위의 점 $\left( a, 0\right)$으로 나타낼 수 있다. 따라서 복소평면에서 $xy$평면의 $x$축에 해당하는 것을 실수축 $Real$ 이라고 한다.
복소평면 위에서 순허수 $bi=0+bi$는 $y$축 위의 점 $\left( 0, b\right)$으로 나타낼 수 있다. 따라서 복소평면에서 $xy$평면의 $y$축에 해당하는 것을 허수축 $Imaginary$ 이라고 한다.
