복소수의 곱셈과 나눗셈

 

단위 복소수의 성질

 

모든 복소수는 그 절댓값과 편각을 이용하여 단위 복소수의 실수배 형태로 나타낼 수 있다. 자세한 내용은 다음의 글을 참고하자.

 

복소수의 극형식 (Polar Form of Complex Number)

 

그렇기 때문에 단위 복소수 간의 연산이 어떻게 이루어지는 지를 파악하면 이를 자연스럽게 복소수 전체 집합에서의 원소들 간 연산으로 확장시킬 수 있다.

 

 

켤레복소수 $\overline{e^{i\theta}}$

 

삼각함수는 다음과 같은 성질을 가지고 있다.

 

이와 같은 성질과 켤레복소수의 정의에 의해, 단위 복소수 $e^{i\theta}$와 그 켤레복소수 $\overline{e^{i\theta}}$는 아래와 같은 관계식을 가진다.

$$ \overline{e^{i\theta}} =\cos\theta -i\sin\theta =\cos\left( -\theta\right) +i\sin\left( -\theta\right) =e^{-i\theta} $$

$$ e^{i\theta}e^{-i\theta}=e^{i\theta}\overline{e^{i\theta}} ={\left| e^{i\theta}\right|}^2=1,\ \ e^{-i\theta}=\frac{1}{e^{i\theta}} $$

(덧붙여 설명하자면 식을 유도할 때 지수법칙을 활용해도 된다고 생각할 수 있지만, 지수가 복소수 범위일 때 실수 범위에서의 지수법칙이 동일하게 성립하는지 증명하지 않았으므로 위와 같이 전개하는 것이 타당하다고 볼 수 있다.)

 

 

 

 

단위 복소수의 곱과 몫

 

편각이 각각 $x$, $y$인 두 단위 복소수 $e^{ix}$, $e^{iy}$를 생각해보면, $e^{ix}$와 $e^{iy}$의 곱은 다음과 같다.

$$ \begin{align} e^{ix}e^{iy} &= \left(\cos x+i\sin x\right)\left(\cos y+i\sin y\right) \\ &= \left(\cos x\cos y-\sin x\sin y\right) +i\left(\cos x\sin y+\sin x\cos y\right) \\ &= \cos\left( x+y\right) +i\sin\left( x+y\right) =e^{i\left( x+y\right)} \end{align} $$

 

마찬가지로 $e^{ix}$와 $e^{iy}$의 나눗셈에 의한 몫은 다음과 같다.

$$ \begin{align} \frac{e^{ix}}{e^{iy}} &= e^{ix}e^{-iy}=\left(\cos x+i\sin x\right)\left(\cos y-i\sin y\right) \\ &= \left(\cos x\cos y+\sin x\sin y\right) +i\left(-\cos x\sin y+\sin x\cos y\right) \\ &= \cos\left( x-y\right) +i\sin\left( x-y\right) =e^{i\left( x-y\right)} \end{align} $$

 

위의 결과로부터 단위 복소수의 곱과 몫 또한 단위 복소수임을 알 수 있다. 뿐만 아니라 단위 복소수에 편각이 $\theta$인 단위복소수 $e^{i\theta}$를 곱해주면 원래 단위 복소수의 편각이 $\theta$만큼 증가한다는 것 또한 알아낼 수 있다.

두 단위 복소수의 곱

 

 

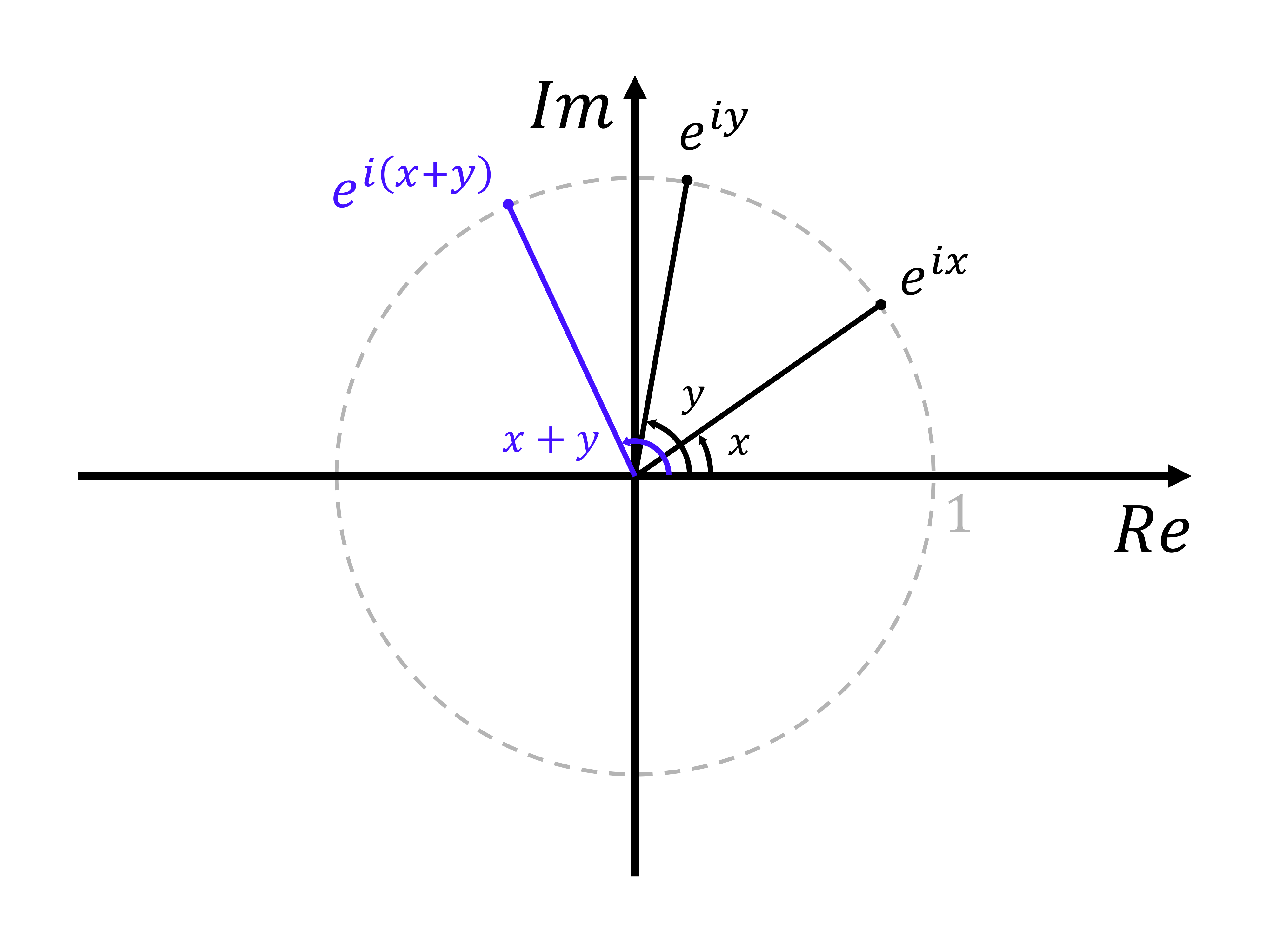
복소수의 곱셈과 나눗셈

 

절댓값이 $r$이고 편각이 $\theta$인 복소수 $z$는 단위 복소수 $e^{i\theta}$에 그 절댓값 $r$만큼 실수배한 것으로 표현할 수 있다. 따라서 임의의 두 복소수 $z_1$, $z_2$를 다음과 같이 나타낼 수 있다.

$$ z_1=r_1e^{i{\theta}_1} ,\quad z_2=r_2e^{i{\theta}_2} $$

 

단위 복소수의 곱셈을 이용하면, $z_1$과$z_2$의 곱은 다음과 같다.

$$ z_1z_2=r_1e^{i{\theta}_1}\times r_2e^{i{\theta}_2}=r_1r_2e^{i{\theta}_1}e^{i{\theta}_2}=r_1r_2\times e^{i\left({\theta}_1+{\theta}_2\right)} $$

따라서 $z_1$과 $z_2$의 곱 $z_1z_2$의 절댓값과 편각은 아래와 같다.

$$ \left| z_1z_2\right| =\left| z_1\right|\left|z_2\right|,\quad\arg\left(z_1z_2\right) =\arg\left( z_1\right) +\arg\left( z_2\right) $$

 

단위 복소수의 나눗셈을 이용하면, $z_1$과$z_2$의 나눗셈에 의한 몫은 다음과 같다.

$$ \frac{z_1}{z_2}=\frac{r_1e^{i{\theta}_1}}{r_2e^{i{\theta}_2}} =\frac{r_1}{r_2}\frac{e^{i{\theta}_1}}{e^{i{\theta}_2}}=\frac{r_1}{r_2}\times e^{i\left({\theta}_1-{\theta}_2\right)} $$

따라서 $z_1$과 $z_2$의 나눗셈에 의한 몫 $\frac{z_1}{z_2}$의 절댓값과 편각은 아래와 같다.

$$ \left|\frac{z_1}{z_2}\right| =\frac{\left| z_1\right|}{\left|z_2\right|},\quad\arg\left(\frac{z_1}{z_2}\right) =\arg\left( z_1\right) -\arg\left( z_2\right) $$