[미분] 2. 여러가지 미분법

 

실수배, 합, 차, 곱, 몫의 미분법

미분가능한 두 함수 $f(x)$와 $g(x)$의 사칙연산으로 이루어진 함수의 도함수는 아래의 미분법을 통해 간단히 구할 수 있다.

 

 

실수배

임의의 실수 $c$에 대해 함수 $y=c \cdot f(x)$ 의 도함수를 구하면

$$\{c \cdot f(x)\}'=\lim_{h \to 0}\frac{c \cdot f(x+h) - c \cdot f(x)}{h}=c \cdot \lim_{h \to 0}\frac{f(x+h)-f(x)}{h}=c \cdot f'(x)$$

 

 

합차

$$\begin{align} \{f(x) \pm g(x)\}' &=\lim_{h \to 0}\frac{\{f(x+h) \pm g(x+h)\}-\{f(x) \pm g(x)\}}{h} \\ &= \lim_{h \to 0}\left(\frac{f(x+h)-f(x)}{h} \pm \frac{g(x+h)-g(x)}{h}\right) \\ &=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h} \pm \lim_{h \to 0}\frac{g(x+h)-g(x)}{h}=f'(x) \pm g'(x) \end{align}$$

 

 

곲의 미분법

$$\begin{align} \{f(x)g(x)\}' &=\lim_{h \to 0}\frac{f(x+h)g(x+h)-f(x)g(x)}{h} \\ &=\lim_{h \to 0}\frac{f(x+h)g(x+h)-f(x)g(x+h)+f(x)g(x+h)-f(x)g(x)}{h} \\ &=\lim_{h \to 0}\frac{\{f(x+h)-f(x)\}g(x+h)+f(x)\{g(x+h)-g(x)\}}{h} \\ &=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h} \times \lim_{h \to 0}g(x+h)+\lim_{h \to 0}f(x) \times \lim_{h \to 0}\frac{g(x+h)-g(x)}{h} \\ &=f'(x)g(x)+f(x)g'(x) \end{align}$$

 

 

몫의 미분법

정의역의 모든 원소 $x$에 대한 함숫값 $g(x) \ne 0$ 인 함수 $g(x)$에 대해

$$\begin{align} \left( \frac{f(x)}{g(x)} \right)' &=\lim_{h \to 0}\frac{\frac{f(x+h)}{g(x+h)}-\frac{f(x)}{g(x)}}{h}=\lim_{h \to 0}\frac{f(x+h)g(x)-f(x)g(x+h)}{h \cdot g(x+h)g(x)} \\ &=\lim_{h \to 0}\frac{f(x+h)g(x+h)-f(x)g(x+h)+f(x)g(x+h)-f(x)g(x)}{h \cdot g(x+h)g(x)} \\ &=\lim_{h \to 0}\frac{g(x)\frac{f(x+h)-f(x)}{h}-f(x)\frac{g(x+h)-g(x)}{h}}{g(x+h)g(x)} \\ &=\lim_{h \to 0}\frac{\{f(x+h)-f(x)\}g(x+h)+f(x)\{g(x+h)-g(x)\}}{h \cdot g(x+h)g(x)} \\ &=\frac{\lim_{h \to 0}g(x) \times \lim_{h \to 0}\frac{f(x+h)-f(x)}{h} - \lim_{h \to 0}f(x) \times \lim_{h \to 0}\frac{g(x+h)-g(x)}{h}}{\lim_{h \to 0}g(x+h) \cdot \lim_{h \to 0}g(x)} \\ &=\frac{f'(x)g(x)-f(x)g'(x)}{\{g(x)\}^2} \end{align}$$

 

 

 

 

합성함수 미분법

$y=f(u)$, $u=g(x)$ 로 두고 합성함수 $y=f(g(x))$ 의 도함수를 구하면

$$\begin{align} \{f(g(x))\}' &=\frac{dy}{dx}=\lim_{\Delta x \to 0}\frac{\Delta y}{\Delta x}=\lim_{\Delta x \to 0}\left(\frac{\Delta y}{\Delta u}\cdot\frac{\Delta u}{\Delta x}\right)=\lim_{\Delta x \to 0}\frac{\Delta y}{\Delta u} \cdot \lim_{\Delta x \to 0}\frac{\Delta u}{\Delta x} \\ &=\lim_{\Delta u \to 0}\frac{\Delta y}{\Delta u} \cdot \lim_{\Delta x \to 0}\frac{\Delta u}{\Delta x}=\frac{dy}{du}\cdot\frac{du}{dx}=f'(u)g'(x)=f'(g(x))g'(x) \end{align}$$

 

 

역함수 미분법

미분가능한 함수 $f(x)$의 역함수 $f^{-1}(x)$가 존재하고 미분가능할 때

$$x=f(y) \leftrightarrow \frac{dx}{dy}=f'(y)$$

이므로 $x=f(y)$ 의 양변을 $x$에 대하여 미분하면

$$1=\frac{d}{dx} f(y)=\frac{d(f(y)}{dy} \frac{dy}{dx}=f'(y) \times \frac{dy}{dx}$$

이므로

$$\frac{dy}{dx}=\frac{1}{f'(y)}=\frac{1}{f'(f^{-1}(x))}, \frac{dy}{dx}=\frac{1}{\frac{dx}{dy}}$$

 

 

매개변수 미분법

두 변수 $x$, $y$의 함수 관계가 변수 $t$를 매개로 하여 $x=f(t)$, $y=g(t)$ 의 꼴로 주어질 때, 변수 $t$를 매개변수라고 하고, 함수 $x=f(t)$, $y=g(x)$ 를 매개변수로 나타내어진 함수라고 한다.

 

매개변수로 나타내어진 함수 $x=g(t)$, $y=h(t)$ 에 대하여 $\frac{dx}{dt} \ne 0$ 인 경우 함수 $y=f(x)$ 의 도함수를 구하면

$$h(t)=f(g(t))$$

양변을 $t$에 대해서 미분하면

$$\frac{d(h(t))}{dt}=\frac{d(f(g(t)))}{d(g(t))} \cdot \frac{d(g(t))}{dt}=\frac{d(f(x))}{dx} \cdot \frac{d(g(t))}{dt}$$

이므로

$$\frac{dy}{dx}=\frac{d(f(x))}{dx}=\frac{\frac{d(h(t))}{dt}}{\frac{d(g(t))}{dt}}=\frac{\frac{dy}{dt}}{\frac{dx}{dt}}$$

 

 

 

 

음함수 미분법

두 변수 $x$, $y$의 관계가 $y=f(x)$ 꼴로 정의될 수 있는 양함수(explicit function)와는 달리 두 변수의 관계가 $f(x, y)=0$ 꼴의 관계식으로 주어질 때, $y$를 $x$의 음함수(implicit function)라고 한다.

 

원, 타원, 포물선, 쌍곡선과 같은 이차곡선은 모두 좌표평면에서 음함수 형태의 관계식으로 나타내어 진다.

 

음함수 미분법은 이러한 도형의 방정식에서 접선의 기울기를 구하거나, $y=f(x)$ 의 형태로 전개하기 어렵고 그 형태가 복잡한 함수들을 미분할 때 주로 이용된다.

 

음함수 미분법의 핵심은 $f(x, y)=0$ 의 관계식에서 $y$를 $x$에 대한 함수로 생각하여 관계식의 모든 항을 $x$에 대해 미분하여 $\frac{dy}{dx}$를 구하는 것이다.

 

아래의 포물선 방정식의 $\frac{dy}{dx}$를 구하는 과정을 통해 음함수 미분법을 설명해보면,

$y^2-x+1=0$ 방정식의 그래프

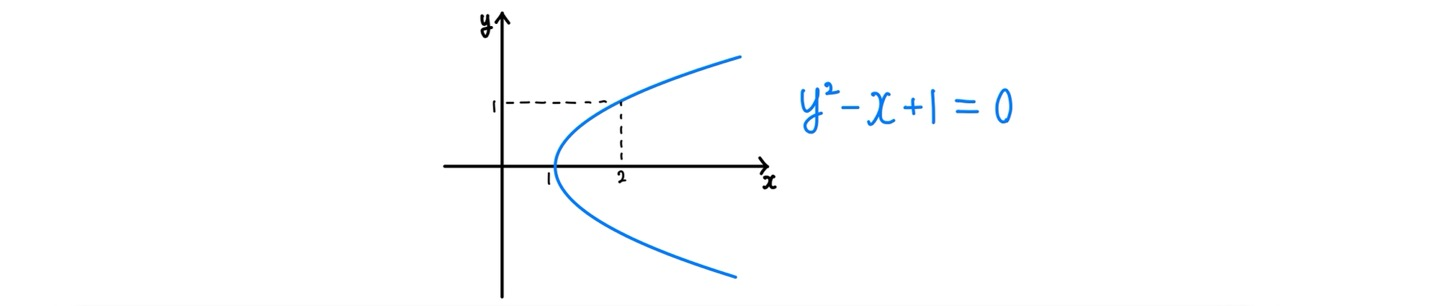
$y^2-x+1=0$ 관계식의 모든 항을 $x$에 대해 미분하면

$$\frac{d}{dx}y^2-\frac{d}{dx}x=\frac{d(y^2)}{dy}\cdot\frac{dy}{dx}-1=2y\frac{dy}{dx}-1=0$$

즉,

$$\frac{dy}{dx}=\frac{1}{2y}$$

가 된다. 이는 곧 포물선 $y^2-x+1=0$ 위의 점 $(\alpha, \beta)$에서의 접선의 기울기가 $\frac{1}{2\beta}$ 임을 의미한다.

 

 

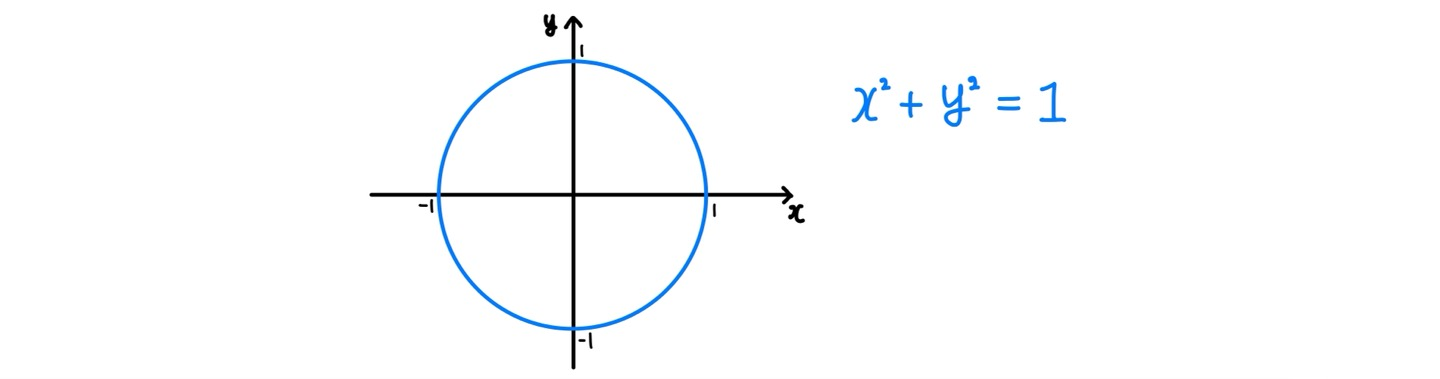
원의 방정식에서도 마찬가지로 $x^2+y^2-1=0$ 관계식의 모든 항을 $x$에 대해 미분하면

$$\frac{d}{dx}x^2+\frac{d}{dx}y^2=\frac{d(x^2)}{dx}+\frac{d(y^2)}{dy}\cdot\frac{dy}{dx}=2x+2y\frac{dy}{dx}=0$$

즉,

$$\frac{dy}{dx}=-\frac{x}{y}$$

가 된다. 이는 곧 원 $x^2+y^2=1$ 위의 점 $(\alpha, \beta)$에서의 접선의 기울기가 $-\frac{\alpha}{\beta}$ 임을 의미한다.

 

 

$xy=2$ 관계식과 같이 $x$와 $y$가 곱셈으로 결합해있는 경우에는 $y$를 $x$에 대한 함수로 생각하여 곱의 미분법을 이용해 $\frac{d}{dx}xy=\frac{d(x)}{dx}y+x\frac{dy}{dx}=y+x\frac{dy}{dx}$ 와 같이 계산하면 된다. 곧,

$$\frac{d}{dx}xy=\frac{d(x)}{dx}y+x\frac{dy}{dx}=y+x\frac{dy}{dx}=0$$

즉,

$$\frac{dy}{dx}=-\frac{y}{x}$$

가 된다. 이는 도형 $xy=2$ 위의 점 $(\alpha, \beta)$에서의 접선의 기울기가 $-\frac{\beta}{\alpha}$ 임을 의미한다.

 

 

 

 

로그 미분법

 

$$y=x^x$$

$$y=x^{\sin x}$$

위와 같이 $y$가 $\{f(x)\}^{g(x)}$ 꼴의 식으로 나타내어지는 경우, 앞서 설명한 미분법들을 적용하여 풀 수 없는 경우에 우리는 로그 미분법을 이용하여 복잡한 함수를 미분할 수 있다.

 

정의역의 모든 $x$에 대해 $f(x)>0$, $g(x)\ge 0$ 인 두 함수 $f(x)$, $g(x)$가 있을 때, 함수 $y=\{f(x)\}^{g(x)}$ 의 도함수를 구하기 위해 양변에 자연로그를 취한다.

$$\ln y=\ln[\{f(x)\}^{g(x)}]=g(x)\cdot\ln f(x)$$

양변을 $x$에 대하여 미분한 뒤 $y$를 이항하면 다음과 같은 도함수를 얻을 수 있다.

$$\frac{d}{dx}\ln y=\frac{1}{y}\frac{dy}{dx}=\frac{d}{dx}g(x)\cdot\ln f(x)+\frac{g(x)}{f(x)}\cdot\frac{d}{dx}f(x)=g'(x)\ln f(x)+\frac{g(x)f'(x)}{f(x)}$$

$$\frac{dy}{dx}=g'(x)\ln f(x)\times y+\frac{g(x)f'(x)}{f(x)}\times y=g'(x)\ln f(x)\{f(x)\}^{g(x)}+\frac{g(x)f'(x)}{f(x)}\{f(x)\}^{g(x)}$$

 

이렇게 구한 일반적인 공식을 이용하여 처음의 두 함수는 각각 다음과 같은 도함수를 가지게 된다.

$$\frac{d}{dx}x^x=\{\ln x+1\}x^x$$

$$\frac{d}{dx}x^{\sin x}=\{x\ln x\cos x+\sin x\}x^{\sin x-1}$$

 

미분과 도함수