[적분] 3. 치환적분 기법 (삼각치환, 반각치환)

 

치환적분 글에서 다루었던 방법들로는 적분하기 어려운 함수들도 존재한다. 그러한 함수들은 삼각치환이나 반각치환을 이용하여 풀 수 있다.

[적분] 2. 치환적분

 

 

삼각치환

삼각치환이란 다음의 두 삼각함수들의 항등식을 이용하여 함수를 적분하는 방법이다.

$$\sin ^2x+\cos ^2x=1$$

$$\tan ^2x+1=\sec ^2x$$

예시를 하나 들어보자. 함수 $f(x)=\frac{1}{x^2+1}$은 분모를 다른 문자로 치환하는 방법으로는 적분할 수 없다. 여기서 $-\frac{\pi}{2}<\theta<\frac{\pi}{2}$일 때, $x=\tan\theta$ 로 치환하면 $dx=\sec ^2\theta d\theta$ 이므로

$$\int_{}{}\frac{1}{x^2+1}\, dx=\int_{}{}\frac{\sec ^2\theta}{\tan ^2\theta +1}\, d\theta=\int_{}{}1\, d\theta=\theta +C=\arctan x+C$$

함수가 $x$에 관한 식이었으므로 부정적분 또한 아크탄젠트 함수를 이용해 $x$에 관하여 나타내었다.

 

이와 같이 $x^2\pm a^2$ 형태의 항을 포함하면서 근호$\surd$ 안에 있거나 인수분해가 불가능한 함수의 경우 다음과 같이 삼각치환하여 풀 수 있다.

$$a^2-x^2\Longrightarrow x=a\sin\theta\quad\left( -\frac{\pi}{2}\le\theta\le\frac{\pi}{2}\right)$$

$$a^2+x^2\Longrightarrow x=a\tan\theta\quad\left( -\frac{\pi}{2}<\theta<\frac{\pi}{2}\right)$$

$$x^2-a^2\Longrightarrow x=a\sec\theta\quad\left( 0\le\theta\le\pi, \theta\ne\frac{\pi}{2}\right)$$

 

 

 

 

반각치환

반각치환이란 $\tan\frac{\theta}{2}=t$ 로 치환하여 삼각함수로 이루어진 함수의 식을 다항식으로 바꾸어 함수를 적분하는 방법이다. 이 때, 각 삼각함수들은 삼각함수의 덧셈정리를 이용하여 다음과 같이 $t$에 대한 식으로 나타낼 수 있다.

$$\sin\theta=2\sin\frac{\theta}{2}\cos\frac{\theta}{2}=2\tan\frac{\theta}{2}\times\frac{1}{\sec ^2\frac{\theta}{2}}=\frac{2\tan\frac{\theta}{2}}{1+\tan\frac{\theta}{2}}=\frac{2t}{1+t^2}$$

$$\cos\theta=2\cos ^2\frac{\theta}{2} -1=\frac{2}{\sec ^2\frac{\theta}{2}}-1=\frac{2}{1+\tan ^2\frac{\theta}{2}}-1=\frac{2}{1+t^2}-1=\frac{1-t^2}{1+t^2}$$

$$\tan\theta=\frac{2\tan\frac{\theta}{2}}{1-\tan ^2\frac{\theta}{2}}=\frac{2t}{1-t^2}$$

 

다음의 그림을 통해서도 삼각함수들을 $t$에 대한 식으로 나타낼 수 있다.

직각삼각형을 이용한 반각치환 증명

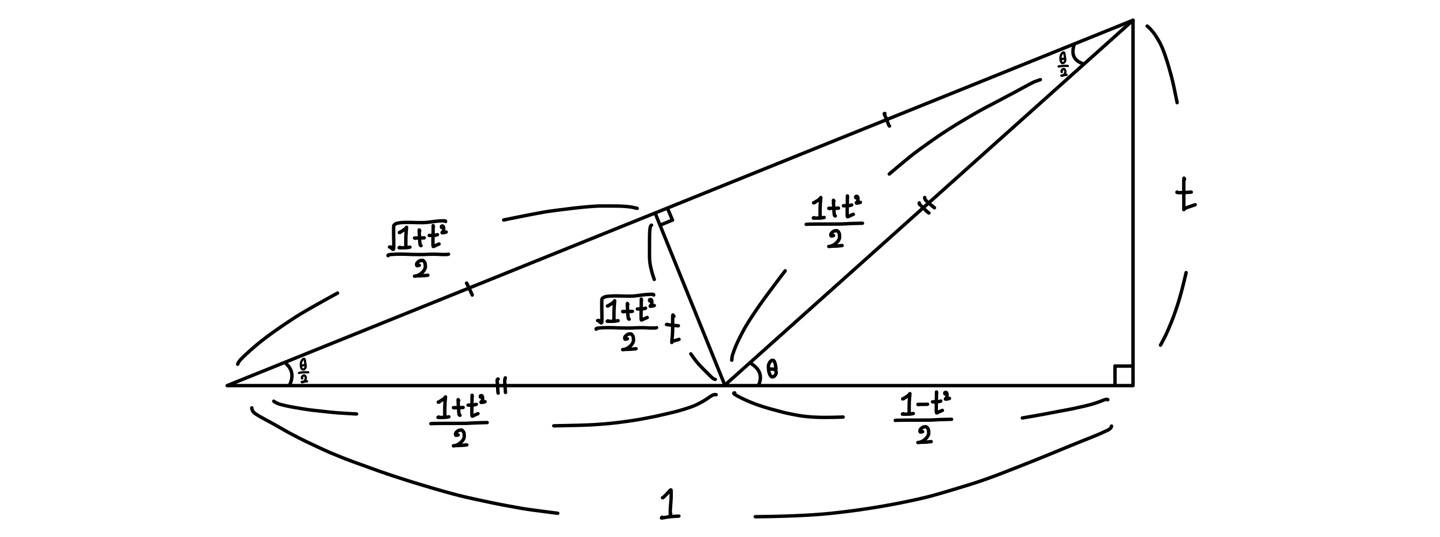
$$\sin\theta=t\times\frac{2}{1+t^2}=\frac{2t}{1+t^2}$$

$$\cos\theta=\frac{1-t^2}{2}\times\frac{2}{1+t^2}=\frac{1-t^2}{1+t^2}$$

$$\tan\theta=t\times\frac{2}{1-t^2}=\frac{2t}{1-t^2}$$

 

마찬가지로 반각치환을 이용하여 예제를 풀어보겠다. 일반적으로 함수 $f(x)=\sec x$의 부정적분을 구하는 것은 아래의 방법이 널리 알려져있다.

$$\int_{}{}\sec x\, dx=\int_{}{}\frac{\sec ^2x+\sec x\tan x}{\sec x+\tan x}\, dx=\int_{}{}\frac{\left(\sec x+\tan x\right)'}{\sec x+\tan x}\, dx=\ln\mid\sec x+\tan x\mid +C$$

이를 $\tan\frac{x}{2}=t$ 로 치환하면 $\frac{1}{2}\sec ^2\frac{x}{2}=\frac{dt}{dx}\Longrightarrow dx=2\cos\frac{x}{2}dt=\left( 1+\cos x\right) dt=\frac{2}{1+t^2}dt$ 이므로

$$\begin{align} \int_{}{}\sec x\, dx &= \int_{}{}\frac{1+t^2}{1-t^2}\frac{2}{1+t^2}\, dt=\int_{}{}\frac{2}{1-t^2}\, dt=\int_{}{}\left(\frac{1}{1-t}+\frac{1}{1+t}\right)\, dt \\ &=-\ln\mid 1-t\mid+\ln\mid 1+t\mid +C= \ln\mid\frac{1+t}{1-t}\mid +C=\ln\mid\frac{1+\tan\frac{x}{2}}{1-\tan\frac{x}{2}}\mid +C \end{align}$$

 

적분