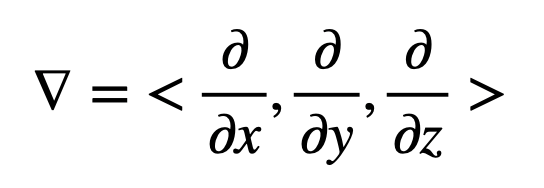최신 글
-
![역행렬 & 가역행렬의 정의와 성질 (with. 계수행렬)]()
역행렬 & 가역행렬의 정의와 성질 (with. 계수행렬)
가역행렬이란행렬의 종류 & 단위행렬 정사각행렬 : 행의 개수 $m$과 열의 개수 $n$이 같은 행렬$n$차 정사각행렬 : 행의 개수와 열의 개수가 $n$인 $n\times n$ 행렬 대각성분 : 정사각행렬의 $\left( i, i\right)$ - 성분 (단, $i=1, 2, 3, \cdots $)대각행렬 : 대각성분을 제외한 모든 성분이 $0$인 행렬 단위행렬 : 대각성분이 모두 $1$인 대각행렬 단위행렬은 기호 $I$로 표기하거나 그 크기를 나타내기 위해 $n$차 단위행렬의 경우 $I_n$과 같이 나타낸다. 가역행렬의 정의 가역행렬과 역행렬은 함께 정의된다. 둘의 정의는 아래와 같다.정사각행렬 $A$에 대해 $AB=I=BA$ 을 만족하는 정사각행렬 $B$가 존재하면 $A$를 가역행렬, $B$를 $A..
-
![가우스 소거법 (Gaussian Elimination) - 기본행연산과 기약 행사다리꼴]()
가우스 소거법 (Gaussian Elimination) - 기본행연산과 기약 행사다리꼴
Linear Equation 연립일차방정식의 풀이법을 알아보기 전에, Linear algebra에서 주로 다루게 되는 Linear equation에 대해서 간단히 소개하고자 한다. Linear equation이란$$ a_1x_1 + a_2x_2 + a_3x_3 + \cdots + a_nx_n = b $$형태의 방정식을 말하며 아래의 세 가지 조건을 만족한다. $a_1$, $a_2$, $a_3$, $\cdots$, $a_n$, $b$ : const.$a_1$, $a_2$, $a_3$, $\cdots$, $a_n$ is not all zero$x_1$, $x_2$, $x_3$, $\cdots$, $x_n$ : variables직관적으로 보았을 때 변수들이 서로 상수곱과 덧셈으로 결합되어..
-
![복소수의 곱셈과 나눗셈]()
복소수의 곱셈과 나눗셈
단위 복소수의 성질 모든 복소수는 그 절댓값과 편각을 이용하여 단위 복소수의 실수배 형태로 나타낼 수 있다. 자세한 내용은 다음의 글을 참고하자. 복소수의 극형식 (Polar Form of Complex Number)극형식 Polar Form 복소수의 절댓값과 편각을 사용하여 복소 공간에서 복소수를 표현하는 방법을 극형식이라고 한다. 복소평면 위에 $0$이 아닌 복소수 $z$가 나타내는 점을 $P\left( z\right)$, 원점을 $Olyssion-studynote.tistory.com 그렇기 때문에 단위 복소수 간의 연산이 어떻게 이루어지는 지를 파악하면 이를 자연스럽게 복소수 전체 집합에서의 원소들 간 연산으로 확장시킬 수 있다. 켤레복소수 $\overline{..
스테디셀러
-
![복소수의 절댓값과 복소평면에서의 거리]()
복소수의 절댓값과 복소평면에서의 거리
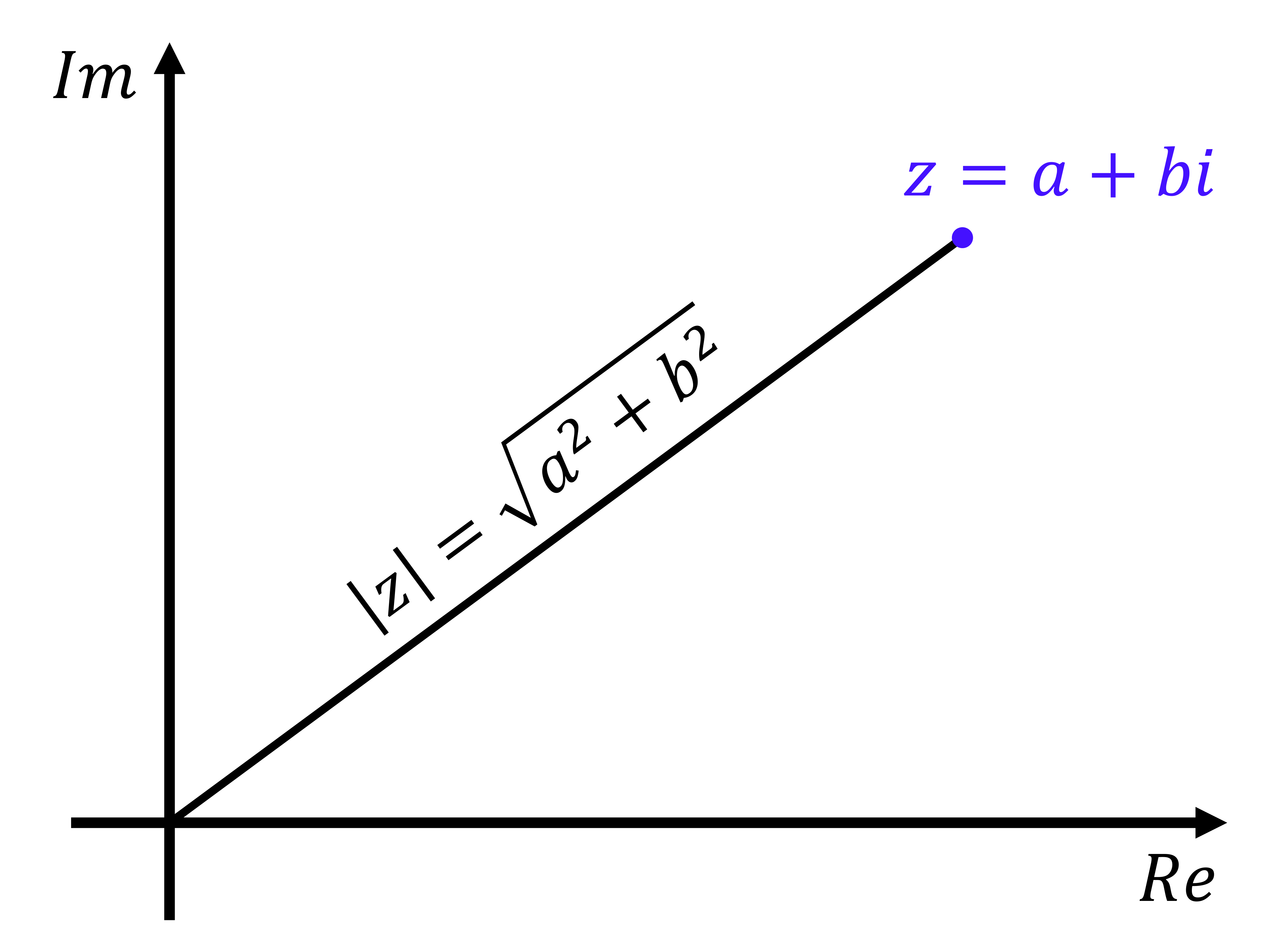
절댓값의 정의 실수의 경우 두 수가 주어졌을 때, 둘 사이의 대소관계를 분명히 알아낼 수 있다. 하지만 허수의 경우 두 수의 대소관계를 말할 수 없다. 그러나 복소수의 절댓값이라는 개념을 도입하면 복소수의 경우에도 절댓값의 크기를 비교할 수 있게 된다. 복소수 $z=a+bi$ 에 대해, 절댓값 $\left| z\right|$는 복소평면 위의 점 $P\left( z\right)$ 에서 원점까지의 거리로 정의된다.$$ \left| z\right| =\left| a+bi\right| =\sqrt{a^2+b^2} $$ 절댓값의 성질 복소수의 절댓값에 대하여 다음의 4가지가 성립한다.$\left| Re\left( z\right)\right|\le\left| z\right|$ and $\l..
-
![테일러 급수와 테일러 정리의 증명]()
테일러 급수와 테일러 정리의 증명
테일러 급수미적분학에서, 테일러 급수란 주어진 함수를 정의역의 특정 점에서의 미분계수들을 계수로 하는 다항식의 무한합으로 표현하는 것을 말하며 테일러 전개라고도 부른다. 즉, 여러번 미분가능한 함수 $f(x)$에 대하여 $x=a$에서 $f(x)$에 접하는 멱급수로 표현하는 방법이다.(테일러 급수$\ne$멱급수 이지만 여기서는 간단히 설명하고 넘어가겠다) 테일러 정리어느 구간에서 미분가능한 함수를 유한 테일러 다항식과 근접할수록 $0$에 가까워지는 오차항의 합으로 표현할 수 있다는 것이 테일러 정리이다. 접선을 통해 함수를 근사하는 선형 근사를 일반화한 다항함수 형태라고 생각할 수 있으며, 테일러 급수는 이 테일러 다항식에서 오차항을 없애고 무한차원까지 확장한 것으로 볼 수 있다. ..
-
![테일러 급수를 이용한 오일러 공식의 증명]()
테일러 급수를 이용한 오일러 공식의 증명
오일러 공식실수 $x$에 대하여 다음이 성립한다$e^{ix}=\cos x+i\sin x$수학자 레온하르트 오일러의 이름이 붙은 공식으로 복소수 지수를 정의하는 출발점이 되며, 복소평면 상에서 삼각함수와 지수함수에 대한 관계를 나타낸다. 증명테일러 급수테일러 급수 글을 참고하여라. (adsbygoogle = window.adsbygoogle || []).push({}); 오일러 공식 증명테일러 정리에 의해 $\sin x, \cos x, e^{ix}$ 함수를 다음과 같이 매클로린 급수로 나타낼 수 있다.(허수지수가 정의되지 않았지만, 오일러 공식이 허수지수를 정의하는 데 쓰이므로 넘어간다.)$$ \sin x=x-\frac{x^3}{3!}+\frac{x^5..
-
![복소수와 복소평면 (Complex Number and Complex Plane)]()
복소수와 복소평면 (Complex Number and Complex Plane)
복소수 Complex Number 실수 : 유리수와 무리수를 통튼 것허수 : $x$에 대한 이차방정식 $x^2=-1$의 해 $i$와 실수의 곱으로서 표현되는 수 복소수란 실수와 허수의 합의 꼴로서 표현되는 수이다. 즉 모든 복소수는 두 실수 $a$, $b$에 대하여 아래와 같이 표현된다.$$ a+bi\quad \left( a, b\in\mathbb{R} \right) $$ 복소수 $z=a+bi$에 대해 $a$를 실수부, $b$를 허수부라고 한다.실수는 $b=0$ 인 복소수이고, 허수는 $b\ne 0$ 인 복소수이다. 이때 $a=0$ 이고 $b\ne 0$ 인 복소수를 순허수라고 한다.복소수 $z=a+bi$ 에 대하여 $a-bi$ 를 $z$의 켤레복소수 $\bar{z}$라고 한다.복..
인기
-
![복소수의 절댓값과 복소평면에서의 거리]()
복소수의 절댓값과 복소평면에서의 거리
절댓값의 정의 실수의 경우 두 수가 주어졌을 때, 둘 사이의 대소관계를 분명히 알아낼 수 있다. 하지만 허수의 경우 두 수의 대소관계를 말할 수 없다. 그러나 복소수의 절댓값이라는 개념을 도입하면 복소수의 경우에도 절댓값의 크기를 비교할 수 있게 된다. 복소수 $z=a+bi$ 에 대해, 절댓값 $\left| z\right|$는 복소평면 위의 점 $P\left( z\right)$ 에서 원점까지의 거리로 정의된다.$$ \left| z\right| =\left| a+bi\right| =\sqrt{a^2+b^2} $$ 절댓값의 성질 복소수의 절댓값에 대하여 다음의 4가지가 성립한다.$\left| Re\left( z\right)\right|\le\left| z\right|$ and $\l..
-
![테일러 급수와 테일러 정리의 증명]()
테일러 급수와 테일러 정리의 증명
테일러 급수미적분학에서, 테일러 급수란 주어진 함수를 정의역의 특정 점에서의 미분계수들을 계수로 하는 다항식의 무한합으로 표현하는 것을 말하며 테일러 전개라고도 부른다. 즉, 여러번 미분가능한 함수 $f(x)$에 대하여 $x=a$에서 $f(x)$에 접하는 멱급수로 표현하는 방법이다.(테일러 급수$\ne$멱급수 이지만 여기서는 간단히 설명하고 넘어가겠다) 테일러 정리어느 구간에서 미분가능한 함수를 유한 테일러 다항식과 근접할수록 $0$에 가까워지는 오차항의 합으로 표현할 수 있다는 것이 테일러 정리이다. 접선을 통해 함수를 근사하는 선형 근사를 일반화한 다항함수 형태라고 생각할 수 있으며, 테일러 급수는 이 테일러 다항식에서 오차항을 없애고 무한차원까지 확장한 것으로 볼 수 있다. ..
-
![테일러 급수를 이용한 오일러 공식의 증명]()
테일러 급수를 이용한 오일러 공식의 증명
오일러 공식실수 $x$에 대하여 다음이 성립한다$e^{ix}=\cos x+i\sin x$수학자 레온하르트 오일러의 이름이 붙은 공식으로 복소수 지수를 정의하는 출발점이 되며, 복소평면 상에서 삼각함수와 지수함수에 대한 관계를 나타낸다. 증명테일러 급수테일러 급수 글을 참고하여라. (adsbygoogle = window.adsbygoogle || []).push({}); 오일러 공식 증명테일러 정리에 의해 $\sin x, \cos x, e^{ix}$ 함수를 다음과 같이 매클로린 급수로 나타낼 수 있다.(허수지수가 정의되지 않았지만, 오일러 공식이 허수지수를 정의하는 데 쓰이므로 넘어간다.)$$ \sin x=x-\frac{x^3}{3!}+\frac{x^5..
-
![복소수와 복소평면 (Complex Number and Complex Plane)]()
복소수와 복소평면 (Complex Number and Complex Plane)
복소수 Complex Number 실수 : 유리수와 무리수를 통튼 것허수 : $x$에 대한 이차방정식 $x^2=-1$의 해 $i$와 실수의 곱으로서 표현되는 수 복소수란 실수와 허수의 합의 꼴로서 표현되는 수이다. 즉 모든 복소수는 두 실수 $a$, $b$에 대하여 아래와 같이 표현된다.$$ a+bi\quad \left( a, b\in\mathbb{R} \right) $$ 복소수 $z=a+bi$에 대해 $a$를 실수부, $b$를 허수부라고 한다.실수는 $b=0$ 인 복소수이고, 허수는 $b\ne 0$ 인 복소수이다. 이때 $a=0$ 이고 $b\ne 0$ 인 복소수를 순허수라고 한다.복소수 $z=a+bi$ 에 대하여 $a-bi$ 를 $z$의 켤레복소수 $\bar{z}$라고 한다.복..
-
![[적분] 5. 리만 합과 리만 적분(Rimann Integral)]()
[적분] 5. 리만 합과 리만 적분(Rimann Integral)
정적분의 시작부정적분과 정적분은 마치 동질적인 것처럼 보이지만 이 둘은 미적분학의 기본정리에 의해 엮어질 뿐, 그 시초와 본질이 전혀 다르다. 부정적분이 미분의 역연산으로서 17세기 이후에 만들어진 것과는 대조되게, 정적분은 수천년 전부터 구분구적법이라는 개념으로 존재했다. 원과 같이 곡선을 포함하여 그 넓이를 재기 어려운 도형들의 넓이를 계산하기 위해, 사각형과 같은 쉽게 넓이를 구할 수 있는 도형들의 작은 조각들로 그 넓이를 어림하여 계산하는 것이다. 이후 라이프니츠가 이러한 도형의 개수를 무한히 늘리면 어림의 오차가 없어져 실제와 같아진다는 아이디어로 정리하였고, 최종적으로 베른하르트 리만이 리만 적분이라는 형태로 완성하였다. 리만 합닫힌 구간 $[a, b]$에서 불연속점이 유한개..
-
![[적분] 3. 치환적분 기법 (삼각치환, 반각치환)]()
[적분] 3. 치환적분 기법 (삼각치환, 반각치환)
치환적분 글에서 다루었던 방법들로는 적분하기 어려운 함수들도 존재한다. 그러한 함수들은 삼각치환이나 반각치환을 이용하여 풀 수 있다. [적분] 2. 치환적분치환적분법부정적분은 미분의 역작용이므로 모든 적분 공식과 계산 기법들은 미분 공식에서 파생된다. 치환적분 또한 합성함수의 미분법에서 출발한다. 미분가능한 함수 $f(x)$, $g(x)$에 대해$$ \flyssion-studynote.tistory.com 삼각치환삼각치환이란 다음의 두 삼각함수들의 항등식을 이용하여 함수를 적분하는 방법이다.$$ \sin ^2x+\cos ^2x=1 $$$$ \tan ^2x+1=\sec ^2x $$예시를 하나 들어보자. 함수 $f(x)=\frac{1}{x^2+1}$은 분모를 다른 문자로 치환..
-
![선전하에 의한 전기장 - 직선도선]()
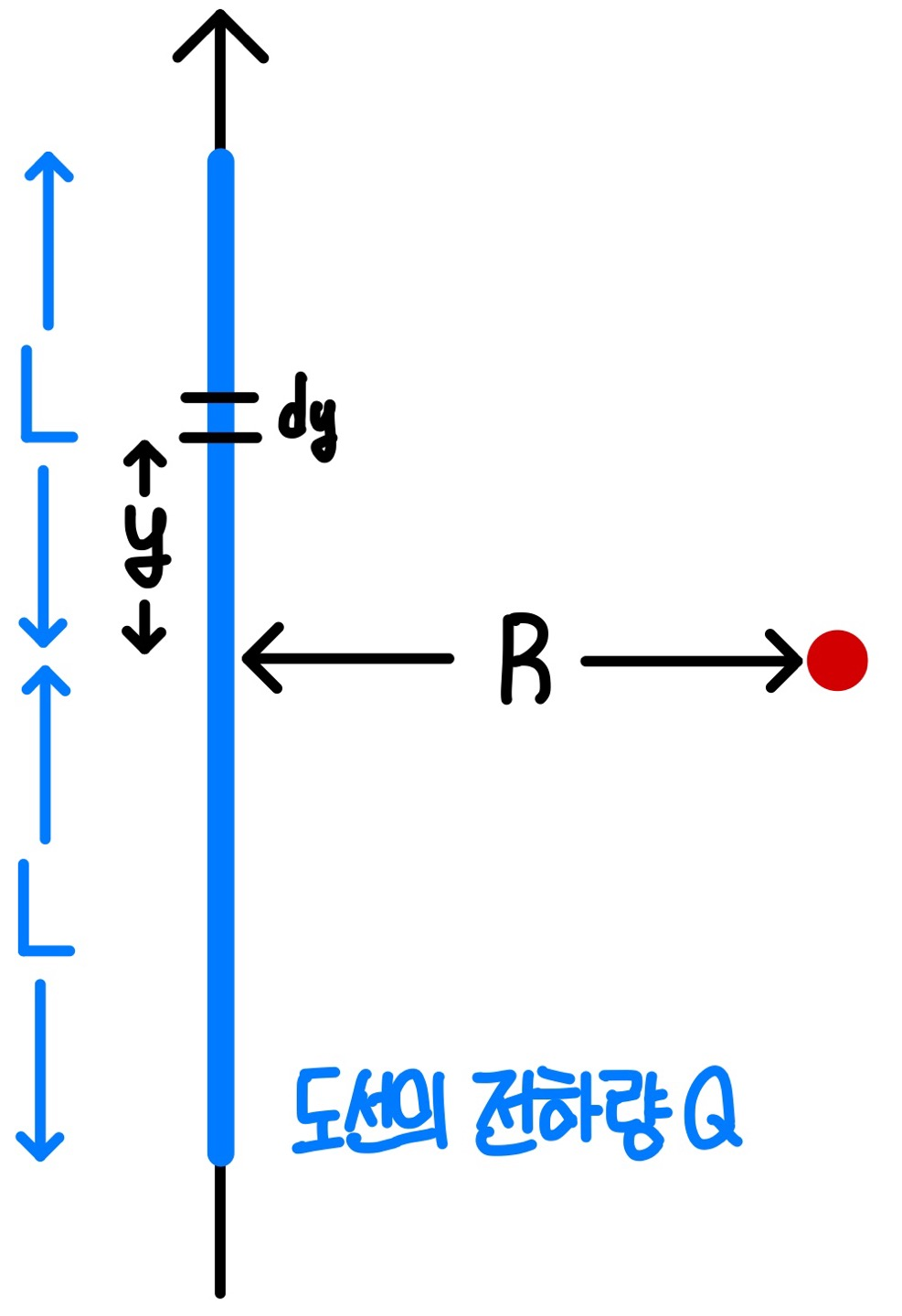
선전하에 의한 전기장 - 직선도선
점전하가 아닌 선전하나 면전하에 의한 전기장을 구할 때는, 선이나 면을 미소단위로 나누어 전기장을 미소점전하들에 의한 전기장의 합으로 생각할 수 있다. 직선 상에 있는 경우그림과 같은 경우에서 도선의 단위길이당 전햐량, 즉 선전하밀도 $\lambda =\frac{Q}{L}$ 이다. 원점 $O$로 부터의 거리를 $x$라 하면, 미소길이 $dx$에서의 전하량 $dQ=\lambda dx$ 이다. 따라서 미소점전하 $dQ$에 의한 전기장 $dE$는 다음과 같다.$$ dE=\frac{1}{4\pi\epsilon _0}\frac{dQ}{x^2}=\frac{1}{4\pi\epsilon _0}\frac{\lambda dx}{x^2} $$직선 도선에 의한 전기장은 이들 미소점전하들의 합이므로 다음과 같..
-
![델 연산자 (Del Operator) - 그래디언트, 다이버전스, 컬, 라플라시안]()
델 연산자 (Del Operator) - 그래디언트, 다이버전스, 컬, 라플라시안
정의 델 연산자는 $\nabla$와 같이 나타내며 아래와 같이 정의된다.$$ \nabla =\sum_{i=1}^n \frac{1}{h_{i}}\frac{\partial}{\partial x_{i}}\hat{x_{i}} $$ 이처럼 델 연산자는 벡터로 취급하여도 무방하다. $h_{i}$는 Scaling Factor이며 극좌표계, 원통좌표계, 구면좌표계와 같이 서로 직교하는 좌표계에서는 $h_{i}$만큼 보정하여 계산한다. 직교좌표계 : $h_{x}=1$, $h_{y}=1$, $h_{z}=1$구면좌표계 : $h_{r}=1$, $h_{\theta}=r$, $h_{\rho}=r\sin\theta$원통좌표계 : $h_{\rho}=1$, $h_{\theta}=r$, $h_{z}=1$ 따라..
-
![복소수의 극형식 (Polar Form of Complex Number)]()
복소수의 극형식 (Polar Form of Complex Number)
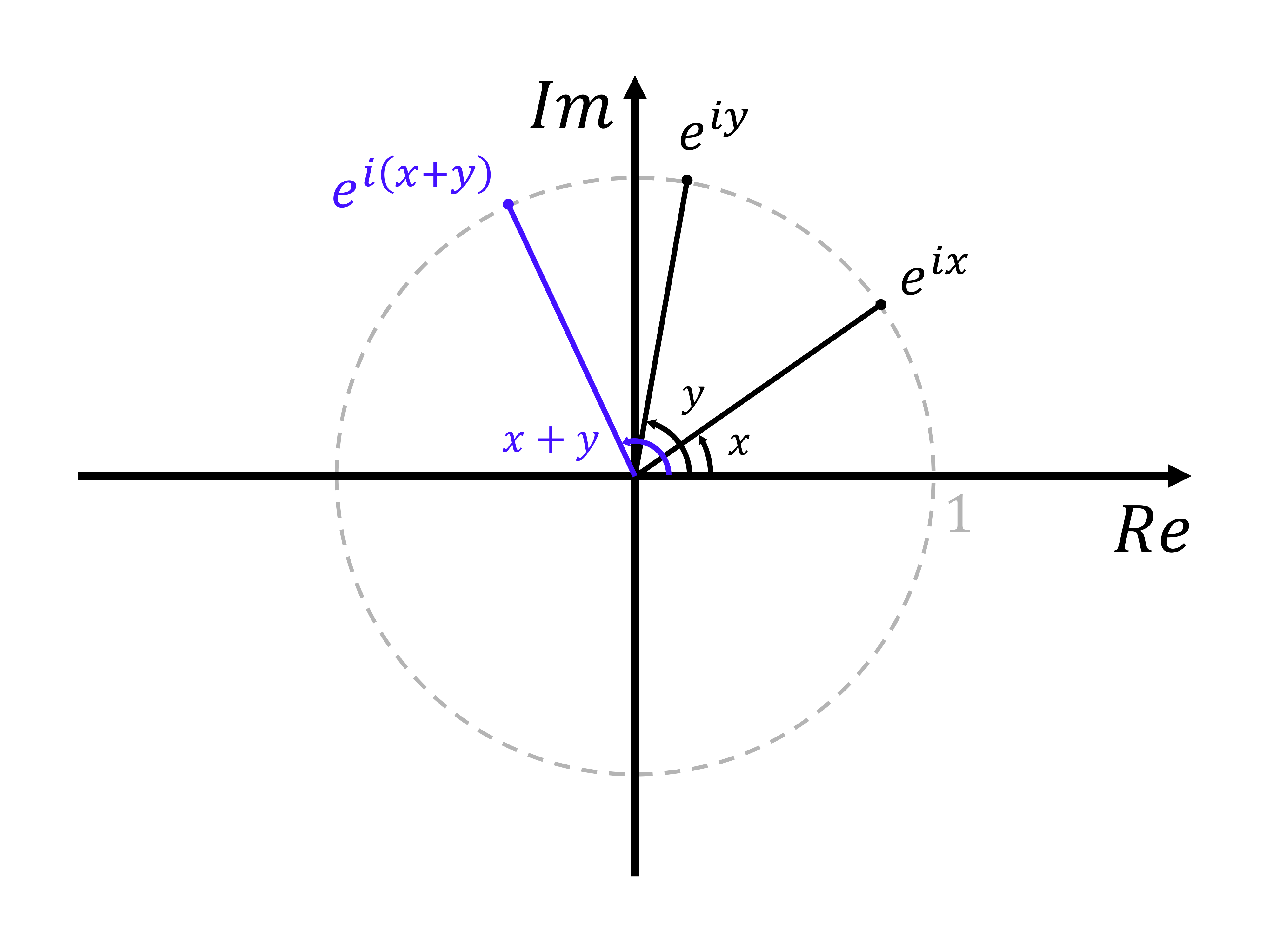
극형식 Polar Form 복소수의 절댓값과 편각을 사용하여 복소 공간에서 복소수를 표현하는 방법을 극형식이라고 한다. 복소평면 위에 $0$이 아닌 복소수 $z$가 나타내는 점을 $P\left( z\right)$, 원점을 $O$라고 할 때, 선분 $\overline{OP}$가 $x$축의 양의 방향과 이루는 각의 크기를 $\theta$로 두면 다음과 같다.$$ Re\left( z\right) =\left| z\right|\cos\theta ,\quad Im\left( z\right) =\left| z\right|\sin\theta $$이를 통해 복소수 $z$를 아래와 같이 나타낼 수 있다.$$ z=\left| z\right|\left(\cos\theta +i\sin\theta\right) ..





![[적분] 5. 리만 합과 리만 적분(Rimann Integral)](https://blog.kakaocdn.net/dn/cRIXOE/btrvKJIJ5Jm/UsIHinQzu4NSMf5Tu9jPGk/img.jpg)
![[적분] 3. 치환적분 기법 (삼각치환, 반각치환)](https://blog.kakaocdn.net/dn/8Vwm0/btrvJ0C2RrA/o2C78u3ruUKh3ekA5oGj81/img.jpg)